Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ta có: BH⊥AH tại H
nên BH là tiếp tuyến của (A;AH) có H là tiếp điểm
Ta có: CH⊥AH tại H
nên CH là tiếp tuyến của (A;AH) có H là tiếp điểm
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm
BM là tiếp tuyến có M là tiếp điểm
Do đó: BH=BM
Xét (A) có
CH là tiếp tuyến có H là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CH=CN
Ta có: BH+CH=BC
nên BC=BM+CN

a: ta có: BH\(\perp\)AH tại H
nên BH là tiếp tuyến của (A;AH) có H là tiếp điểm
Ta có: CH\(\perp\)AH tại H
nên CH là tiếp tuyến của (A;AH) có H là tiếp điểm
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm
BM là tiếp tuyến có M là tiếp điểm
Do đó: BH=BM
Xét (A) có
CH là tiếp tuyến có H là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CH=CN
Ta có: BH+CH=BC
nên BC=BM+CN

b, Vì C là giao 2 tiếp tuyến CH và CN của (A;AH) nên AC là phân giác góc NCH
Vì B là giao 2 tiếp tuyến BH và BM của (A;AH) nên AB là phân giác góc HBM
Do đó \(\widehat{MBC}+\widehat{NCB}=2\left(\widehat{ACH}+\widehat{ABH}\right)=2\cdot90^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên BM//CN
c, Vì BM,CN là tiếp tuyến (A;AH) nên \(BM\perp AM;CN\perp AN\)
Mà BM//CN nên AM trùng AN hay A;M;N thẳng hàng

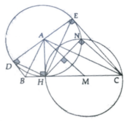
a, Chú ý: Ab là phân giác góc D A M ^ ; AC là phân giác góc E A M ^ từ đó D A E ^ = 180 0
b, Sử dụng tính chất hai tiếp tuyến và hệ thức về đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông BAC => BD.CE = BH.CH = C H 2 = D E 2 4
c, ∆HNC nội tiếp đường tròn (M) đường kính HC => HN ⊥ NC
Chứng minh AN là tiếp tuyến của (M)
Do đó AM ⊥ HN => AM//NC

A H B C M I D K F P Q G Note:Hình hơi lệch xíu ^^
a, Vì CM là tiếp tuyến của (A)
=> \(CM\perp AM\)
=> ^CMA = 90o
=> M thuộc đường tròn đường kính AC
Vì ^CHA = 90o
=> H thuộc đường tròn đường kính AC
Do đó : M và H cùng thuộc đường tròn đường kính AC
hay 4 điểm A,C,M,H cùng thuộc đường tròn đường kính AC
b, Vì AM = AH ( Bán kính)
CM = CH (tiếp tuyến)
=> AC là trung trực MH
=> \(AC\perp MH\)tại I
Xét \(\Delta\)AMC vuông tại M có MI là đường cao
\(\Rightarrow MA^2=AI.AC\)(Hệ thức lượng)
c, Vì CM , CH là tiếp tuyến của (A)
=> AC là phân giác ^HAM
=> ^HAC = ^MAC
Mà ^HAC + ^HAB = 90o
=> ^MAC + ^HAB = 90o
Ta có: ^BAD + ^BAC + ^CAM = 180o (Kề bù)
=> ^BAD + 90o + ^CAM = 180o
=> ^BAD + ^CAM = 90o
Do đó ^BAD = ^BAH (Cùng phụ ^CAM)
Xét \(\Delta\)BAD và \(\Delta\)BAH có:
AB chung
^BAD = ^BAH (cmt)
AD = AH (Bán kính (A) )
=> \(\Delta BAD=\Delta BAH\left(c.g.c\right)\)
=> ^ADB = ^AHB = 90o
\(\Rightarrow BD\perp AD\)
=> BD là tiếp tuyến của (A)
Làm đc đến đây thôi :(
Điểm N đâu