Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

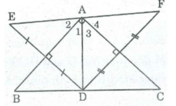
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
⇒ ∠ A 3 = ∠ A 4
∠ (EAF) = ∠ EAD) + ∠ (DAF) = ∠ A 1 + ∠ A 2 + ∠ A 3 + ∠ A 4 = 2( ∠ A 1 + ∠ A 3 ) = 2 . 90 0 = 180 0
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.

* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)

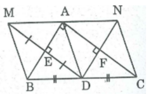
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.

F E B D C A 2 1 3 4
a) E đối xứng với D qua AB=> AD=AE và \(\widehat{A_1}=\widehat{A_2}\)
F đối xứng với D qua AC=> AD=AF và \(\widehat{A_3}=\widehat{A_4}\)
\(\Rightarrow AE=\text{AF}\left(=AD\right),\widehat{DAE}+\widehat{D\text{AF}}=2\left(\widehat{A_1}+\widehat{A_3}\right)=2.90^0=180^0\)=> E,A,F thẳng hàng.
Vậy E đối xứng với F qua A(ĐPCM)
b) Ta có: EF=2AD nên EF nhỏ nhất => AD nhỏ nhất => D là chân đường cao kẻ từ A đến BC

 Võ Hồng Nhung
Võ Hồng Nhung
1 phút trước (15:05)
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AC, AB. Gọi O là 1 điểm bất kì. A' là điểm đối xứng với O qua D, B' là điểm đối xứng với O qua E, C' là điểm đối xứng với O qua F. Chứng minh AA', BB', CC' đồng quy tại 1 điểm.

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
b: Xét tứ giác AMBP có
D là trung điểm chung của AB và MP
MA=MB
Do đó: AMBP là hình thoi
=>ABlà phân giác của góc MAP(1)
c: Xét tứ giác AMCQ có
E là trung điểm chung của AC và MQ
MA=MC
Do đó: AMCQ là hình thoi
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*90=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
 ok!!!!
ok!!!!
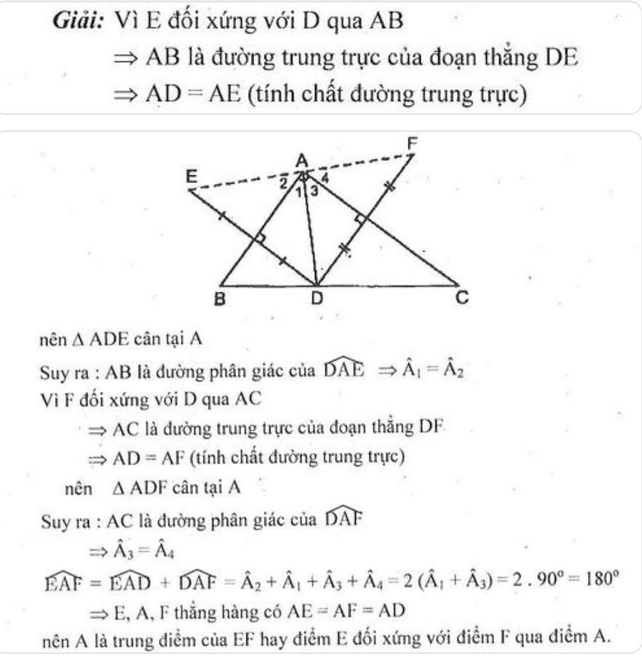
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ΔADE cân tại A
Suy ra: AB là đường phân giác của ∠(DAE) ⇒ ∠A1= ∠A2
* Vì F đối xứng với D qua AC⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ΔADF cân tại A
Suy ra: AC là phân giác của ∠(DAF)
⇒ ∠A3= ∠A4
∠(EAF) = ∠(EAD) + ∠(DAF) = ∠A1+ ∠A2+ ∠A3+ ∠A4= 2(∠A1+ ∠A3) = 2.90o = 180o
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.