Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

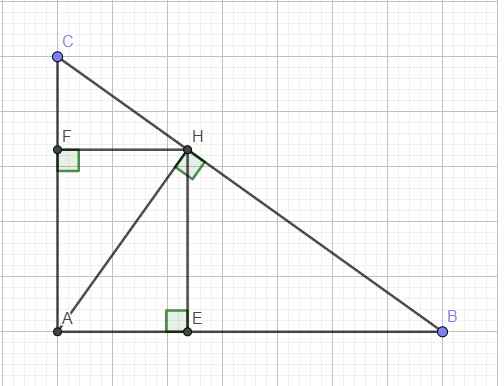
Cho tam giác ABC vuông tại A( AB<AC ), có đường cao AH, trung tuyến AM Gọi E và F lần lượt la hình chiếu của H lên AB và AC; I và K lần lượt là trung điểm của HB và HC. CM :

A B C H E F
a) Sử dụng hệ thức lượng trong các tam giác vuông ABH; ACH và ABC
\(AB.BE=BH^2;AC.CF=CH^2\)
\(AB^2=BH.BC;AC^2=CH.BC\)
=> \(\frac{AB^3}{AC^3}=\frac{BE}{CF}\)
<=> \(\frac{AB^4}{AC^4}=\frac{BE.AB}{CF.AC}=\frac{BH^2}{CH^2}\)
<=> \(\frac{AB^2}{AC^2}=\frac{BH}{CH}\)
<=> \(\frac{BH.BC}{CH.BC}=\frac{BH}{CH}\)
<=> \(\frac{BH}{CH}=\frac{BH}{CH}\) đúng
Vậy ta có điều phải chứng minh là đúng
b)
Ta có: \(AH^2=BH.CH\)
=> \(AH^4=BH^2.CH^2=BE.AB.CF.AC=BE.CF.AB.AC=BE.CF.AH.BC\)
=> \(AH^3=BC.BE.CF\)
c)
Xét tam giác vuông BEH và tam giác vuông HFC
có: ^EBH =^FHC ( cùng phụ góc FCH)
=> Tam giác BEH đồng dạng tam giác HFC
=> \(\frac{BE}{HF}=\frac{EH}{FC}\Rightarrow BE.FC=EH.FH\)
=> \(AH^3=BC.HE.HF\)

Tứ giác AEHF là hình chữ nhật (có 3 góc vuông) \(\Rightarrow HE=AF\)
Áp dụng định lý Pitago trong tam giác vuông AFH:
\(AH^2=AF^2+HF^2=HE^2+HF^2\)
Áp dụng hệ thức lượng trong tam giác vuông AHB với đường cao HF:
\(HF^2=AF.FC\)
Tương tự:
\(HE^2=AE.EB\)
\(\Rightarrow AH^2=HE^2+HF^2=AE.EB+AF.FC\) (đpcm)

a) Tương tự: https://h.vn/hoi-dap/question/392113.html (1)
EH // AC (cùng _I_ AB)
=> \(\widehat{BHE}=\widehat{HCF}\) (2 góc so le trong)
=> \(\Delta EBH\) ~ \(\Delta FHC\) (g - g)
\(\Rightarrow\frac{EB}{FH}=\frac{EH}{FC}\)
\(\Rightarrow EB\times FC=EH\times FH\)
\(\Rightarrow EB\times FC\times BC=BC\times EH\times FH\) (2)
Từ (1) và (2) => đpcm
b)
Thay AH = x và BC = 2a vào \(AH^3=BC\times EH\times FH\), ta có:
\(x^3=2a\times EH\times FH\)
\(\Rightarrow FA\times AE=\frac{x^3}{2a}\) (EH = FA và FH = AE)
\(S_{AEF}=\frac{1}{2}\times FA\times AE=\frac{1}{2}\times\frac{x^3}{2a}=\frac{x^3}{4a}\left(\text{đ}v\text{d}t\right)\)

Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)

b: \(\dfrac{BE}{CF}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}=\dfrac{HB^2}{HC^2}\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)
c: \(BC\cdot BE\cdot CF\)
\(=BC\cdot\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\)
\(=AH^4\cdot\dfrac{BC}{AB\cdot AC}\)
\(=AH^4\cdot\dfrac{BC}{AH\cdot BC}=AH^3\)

bạn tự vẽ hình nha ^.^
trong tam giác vuông ABC có \(AH^2=BH\cdot CH\) \(\Rightarrow AH^4=BH^2\cdot CH^2\)
ma \(HB^2=BE\cdot AB,HC^2=FC\cdot AC\)
suy ra \(AH^4=BE\cdot AB\cdot FC\cdot AC\)
nhung \(AB\cdot AC=AH\cdot BC\)
nen \(AH^4=BE\cdot FC\cdot AH\cdot BC\Rightarrow AH^3=BE\cdot FC\cdot BC\)(1)
de dang chung minh duoc tam giac BEH ~tam giac HFC
suy ra\(\frac{BE}{HF}=\frac{EH}{FC}\Rightarrow BE\cdot FC=EH\cdot HF\)thay vao (1) ta cung co dpcm
cám ơn bạn nhiều nha =)