Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> MN//AC
Mà AC⊥AB(tam giác ABC vuông tại A)
=> MN⊥AB(từ vuông góc đến song song)
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(pytago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)
Ta có: MN là đường trung bình tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)

a: Ta có: ΔABC vuông tại A
mà AP là đường trung tuyến
nên \(AP=\dfrac{BC}{2}=5\left(cm\right)\)
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{1}{2}BC\)
=>\(MN=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
b: Xét ΔABC có
N,P lần lượt là trung điểm của CA,CB
=>NP là đường trung bình của ΔABC
=>NP//AB và \(NP=\dfrac{AB}{2}\)
Ta có: NP//AB
M\(\in\)AB
Do đó: NP//AM
ta có: \(NP=\dfrac{AB}{2}\)
\(AM=\dfrac{AB}{2}\)=MB
Do đó; NP=AM=MB
Xét tứ giác AMPN có
AM//NP
AM=NP
Do đó: AMPN là hình bình hành
Hình bình hành AMPN có \(\widehat{MAN}=90^0\)
nên AMPN là hình chữ nhật

a: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
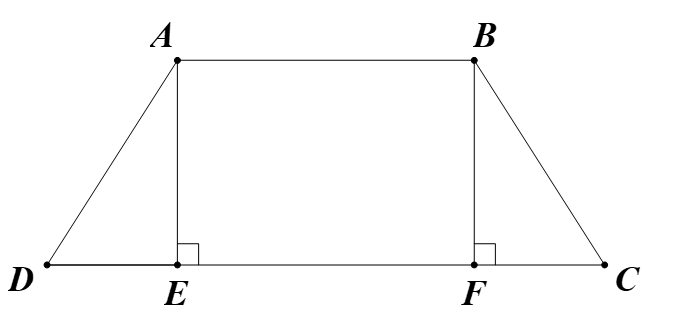
b: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
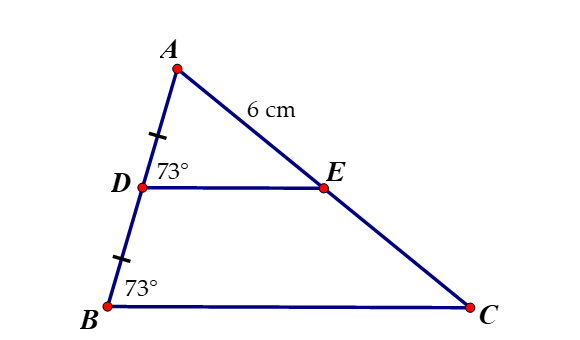
Hình thang BMNC có \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
c: Ta có: \(MN=\dfrac{BC}{2}\)
mà \(MN=\dfrac{MP}{2}\)
nên BC=MP
Ta có: MN//BC
P\(\in\)MN
Do đó: MP//BC
Xét tứ giác MBCP có
MP//BC
MP=BC
Do đó: MBCP là hình bình hành
Sửa đề: Chứng minh AHCQ là hình chữ nhật
Xét tứ giác AHCP có
N là trung điểm chung của AC và HP
=>AHCP là hình bình hành
Hình bình hành AHCP có \(\widehat{AHC}=90^0\)
nên AHCP là hình chữ nhật
d: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔBAC có
H,M lần lượt là trung điểm của BC,BA
=>HM là đường trung bình của ΔBAC
=>HM//AC và HM=AC/2
Tứ giác AMHC có HM//AC
=>AMHC là hình thang
e:
Ta có: \(HM=\dfrac{AC}{2}\)
\(AN=\dfrac{AC}{2}\)
Do đó: HM=AN
Xét tứ giác AMHN có
HM//AN
HM=AN
Do đó: AMHN là hình bình hành
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Ta có: AHCQ là hình chữ nhật
=>AQ//HC và AQ=HC
Ta có: AQ//HC
H\(\in\)BC
Do đó: AQ//HB
ta có: AQ=HC
HB=HC
Do đó: AQ=HB
Xét tứ giác ABHQ có
AQ//BH
AQ=BH
Do đó: ABHQ là hình bình hành
=>AH cắt BQ tại trung điểm của mỗi đường

Câu 1:
Vì M,N là trung điểm AB,BC nên MN là đtb tg ABC
Do đó \(MN=\dfrac{1}{2}AC=8\left(cm\right)\)
Câu 2:
Vì \(\widehat{AEM}=\widehat{AFM}=\widehat{EAF}=90^0\) nên AEMF là hcn

a)ta có MA=MB
NA=NC
=)MN là đường trung bình tam giác ABC
=)MN//BC
b)ta có MN là đường trung bình tam giác ABC (cmt)
=)MN=1/2BC
lại có BC = 10cm (gt)
=)MN=BC/2=5 cm
B A C M N
a) Xét tam giác ABC có :
M là trung điểm của AB
N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC ( định nghĩa )
=> MN // BC ( tính chất )
b) Vì MN là trung bình của tam giác ABC ( chứng minh trên )
\(\Rightarrow MN=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\) ( tính chất )
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN=BC/2=2,5(cm)