Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha
a)Vì tam giác có AB=AE và góc BAE bằng 90 đọ nên tam giác BAE vuông cân mà AM là tia phân giác của góc BAE nên AM cùng là đg cao và là đg trung tuyến của tam giác BAE(tự chúng minh)
Suy ra BM=AM=MC(tính chất đg trung tuyến của tam giác vuông) và góc BMA bằng 90 độ.Do đó tam giác ABM vuông cân(ĐPCM)
b)Xét 2 tam giác BHA và tam giác AIE lần lượt vuông tại H,I có:
BA=AE
góc BAH=góc AEI(vì cùng phụ với góc IAE)
Suy ra tam giác BHA =tam giác AIE(cạnh huyền-góc nhọn kề)
Suy ra IE=AH(đpcm)
c)từ E kẻ đg vuông góc với IE cắt BC tại D,nối M với D
Ta có:IH vuông góc với IE mà ED vuông góc với IE nên IH song song với DE.Suy ra có 2 cặp song song với nhau và cắt nhau đó là HD với IE,IH với ED
Do đó áp dụng t/c đoạn chắn suy ra IE=HD mà IE=AH nên AH =HD
Ta lại có:IH song song vói ED mà IH vuông góc với BC nên ED vuông góc với BC
Suy ra tam giác BDE vuông góc tại D
Xét tam giác BDE có đg trung tuyến MD(vì M là trung điểm của BE(câu A)) nên BM=MD=ME(t/c đg trung tuyến của tam giác vuông)
Mà AM=BM=ME(câua)) nên MA=MD
Suy ra tam giác AHM=tam giác DHM(c.c.c)
Suy ra góc AHM=góc DHM,mà tổng 2 góc này bằng 90 độ nên góc AHM=góc DHM=45 độ(đpcm)

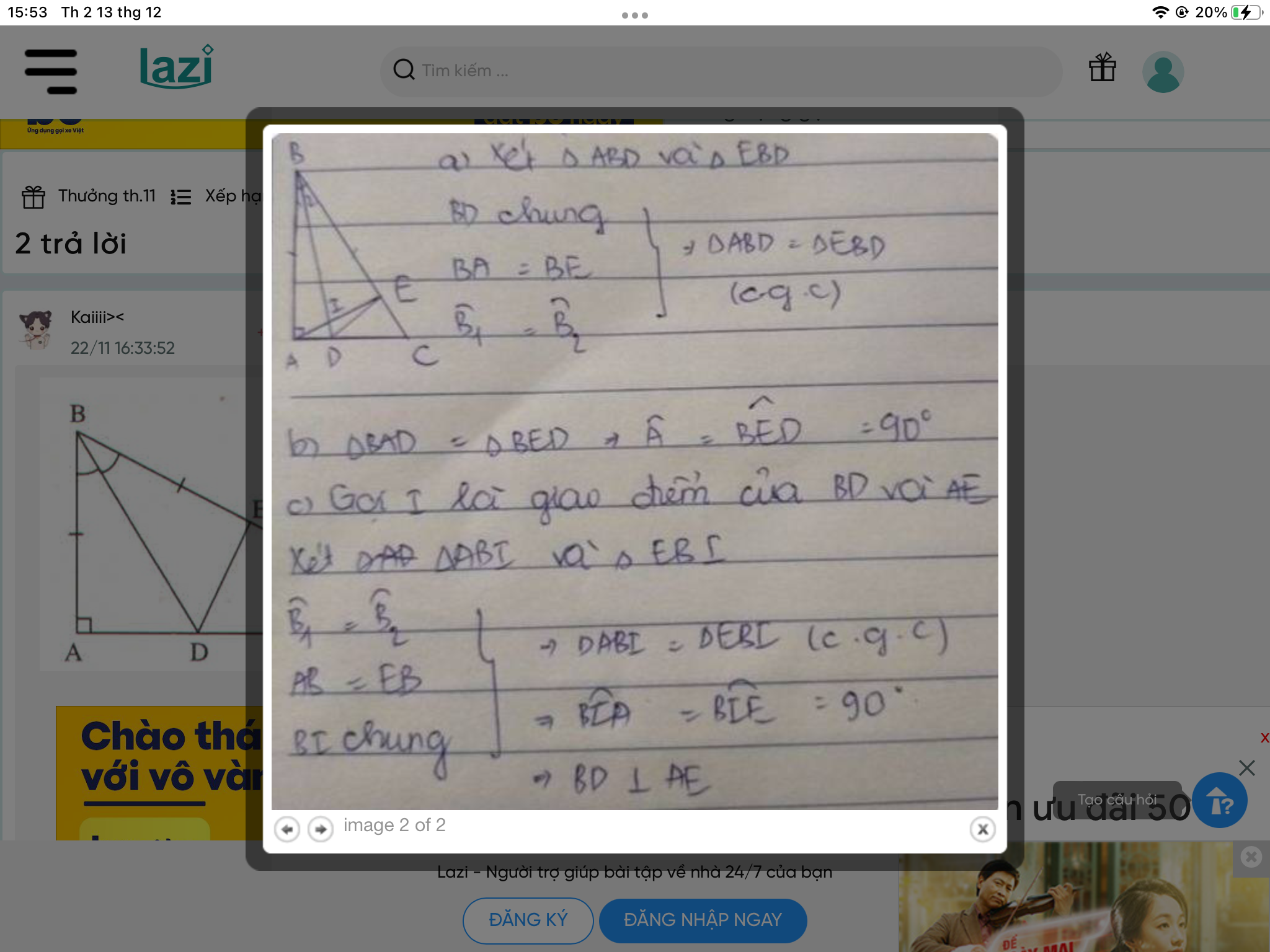
a, xét tam giác ABM và tam giác KBM có: AB=BK, BM chung, góc ABM= góc KBM
suy ra 2 tam giác trên bằng nhau
hok tốt
tu ve hinh :
xet tamgiac ABM va tamgiac KBM co : MB chung
goc ABM = goc MBK do BM la phan giac cua goc ABC (gt)
AB = AK (gt)
=> tammgiac ABM = tamgiac KBM (c - g - c)

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
A B C H I M E
1) Do \(\Delta BAE\)có \(AB=AE\Rightarrow\Delta BAE\)cân vuông tại A
Mà \(AM\)là đường phân giác của \(\Delta BAE\)(hay\(\Delta ABC\))
\(\Rightarrow AM\)đồng thời là đường cao của \(\Delta BAE\Rightarrow\widehat{AMB}=\widehat{AME}=90^0\)
Ta có: \(\widehat{BAM}=\widehat{EAM}=\frac{\widehat{BAE}}{2}=45^0\left(1\right)\).Mà \(\Delta BAE\)vuông cân tại A\(\Rightarrow\widehat{ABM}=\widehat{AEM}=\frac{180^0-\widehat{BAE}}{2}=45^0\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\Delta ABM\)vuông cân (đpcm)
2) Vì \(\Delta ABC\)có \(\widehat{BAC}=90^0\Rightarrow\widehat{ABC}+\widehat{ACB}=180^0-\widehat{BAC}=90^0\left(3\right)\)
Vì H là đường cao của \(\Delta ABC\Rightarrow\widehat{AHC}=90^0\Rightarrow\widehat{HAC}+\widehat{ACH}=180^0-\widehat{AHC}=90^0\)(Hay \(\widehat{HAC}+\widehat{ACB}=90^0\))\(\left(4\right)\)
Từ (3) và (4)\(\Rightarrow\widehat{ABC}=\widehat{HAC}=90^0-\widehat{ACB}\)(Hay \(\widehat{ABH}=\widehat{IAE}\))
Xét \(\Delta ABH\)và\(\Delta EAI\)có:\(\hept{\begin{cases}\widehat{AHB}=\widehat{EIA}=90^0\\AB=AE\\\widehat{ABH}=\widehat{EAI}\end{cases}}\Rightarrow\Delta ABH=\Delta EAI\)(cạnh huyền góc nhọn)
\(\Rightarrow IE=AH\)(Đpcm)