Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: góc HEA = góc EAD = góc ADH (=900)
=> tứ giác AEHD là hình chữ nhật
=> ED = AH.
Gọi T là giao điểm của ED và AH, ta có: ET = TH = TD = AT
Trong tam giác vuông BEH có EM là đường trung tuyến ứng với cạnh huyền BH => EM = MH (1)
Xét tam giác MET và tam giác MHT có:
ME = MH(từ 1); MT chung; ET = TH (chứng minh trên)
=> tam giác MET = tam giác MHT (c-c-c)
=> góc MET= góc MHT =900 (2 góc tương ứng) (2)
Tường tự ta có tam giác HTN = tam giác DTN (c-c-c)
=> góc THN = góc TDN = 900 (2 góc tương ứng) (3)
Từ (2)(3) => EM song song với DN
(vì cùng vuông góc với DE " từ vuông góc đến song song")
=> tứ giác EMND là hình thang và có góc MED = góc EDN (=900)
=> hình thang EMND là hình thang vuông

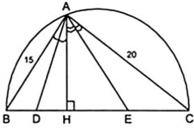
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C 2 = A C + A B 2 ⇒ B C 2 = 15 2 + 20 2 ⇔ B C 2 = 25 2 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
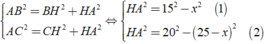
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
15 2 - x 2 - 20 2 + ( 25 - x ) 2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A 2 = 15 2 - 9 2 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
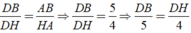
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
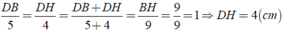
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
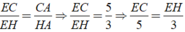
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
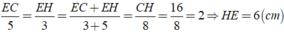

1.Giải:
a. Vì tam giác ABC vuông tại A và AM = \(\frac{1}{2}\)BC
=> AM là đường trung tuyến ứng với cạnh BC
=> M là trung điểm của cạnh BC
=> AM = BM = \(\frac{1}{2}\)BC
Vì AM = BM => Tam giác ABM cân tại M
b. Vì N là trung điểm của AB
=> MN là đường trung tuyến ứng với cạnh AB của tam giác ABM
Mà tam giác ABM cân tại M ( câu a )
=> MN đồng thời là đường cao xuất phát từ M của tam giác ABM
=> \(MN\perp AB\)
Do đó: MN//AC (cùng vuông góc với AB)
=> MNAC là hình thang
Mặt khác: \(\widehat{NAC}\)= \(^{90^0}\)(gt)
=> Tứ giá MNAC là hình thang vuông.

Gọi gđ của ED và HA là O . Ta có:
tam giác MEH cân => góc HEM=MHE
tam giác OEH cân => góc OEH=OHE
mà góc OHE+MHE=90 độ
=> góc HEM+OEH=90 độ
=> EM vuông góc với ED
DN vuông góc với ED => DEMN là hình thang vuông

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE

a) Xét \(\Delta BDF\)và \(\Delta EDC\) có:
\(\widehat{BDF}=\widehat{EDC}=90^0\)
\(\widehat{BFD}=\widehat{ECD}\) (DO CÙNG PHỤ VỚI GÓC ABC )
Suy ra: \(\Delta BDF~\Delta EDC\)
\(\Rightarrow\)\(\frac{BD}{ED}=\frac{DF}{DC}\)
\(\Rightarrow\)\(BD.DC=ED.FD\)
a) Có AB ⊥ AC, HD ⊥ AB
=> HD // AC
=> \(\widehat {DHA} = \widehat {HAC}\)
- Xét tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)
=> ΔHDA ∽ ΔAHC
b) Xét tam giác ABC có: \(A{B^2} + A{C^2} = B{C^2}\)
mà AB=5cm, AC=4cm
=> \(BC = \sqrt {41} \)
- Có AH.BC=AB.AC
=> \(AH = \frac{{20\sqrt {41} }}{{41}}\)
=> \(H{B^2} = A{B^2} - A{H^2}\) (áp dụng định lý Pythagore trong tam giác vuông BHA)
=> \(HB = \frac{{25\sqrt {41} }}{{41}}\)
=> \(HC = \frac{{16\sqrt {41} }}{{41}}\)
- Xét tam giác vuông BDH và tam giác vuông BAC có: HD // AC
=> ΔBDH ∽ ΔBAC
=> \(\frac{{BH}}{{BC}} = \frac{{DH}}{{AC}}\)
=> \(H{\rm{D}} = \frac{{100}}{{41}}\)