Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=10(cm)
b: Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)
nên HB=3,6(cm)
=>HC=BC-HB=6,4(cm)
câu này lúc nãy làm rồi em nhé! ( bổ sung BH )
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)

a.Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.AH: đã có
Áp dụng định lý pitago vào tam giác vuông AHC, có:
\(AC^2=AH^2+CH^2\)
\(\Rightarrow CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

a: \(AB=\sqrt{AH^2+HB^2}=7.5\left(cm\right)\)
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
BC=HB+HC=12,5cm
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A

A B C H 20 cm 9cm 16 cm
*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ACH, ta có :
\(\Rightarrow\)AC2 = HC2 + AH2
\(\Rightarrow\)202 = 162 + AH2
\(\Rightarrow\)AH2 = 400 - 256
\(\Rightarrow\)AH2 = 144
\(\Rightarrow\)AH = 12 (cm)
*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ABH, ta có :
\(\Rightarrow\)AB2 = AH2 + HB2
\(\Rightarrow\)AB2 = 122 + 92
\(\Rightarrow\)AB2 = 225
\(\Rightarrow\)AB = 15 (cm)
Vậy AB = 15 cm; AH = 12 cm

A B C F H K
a, Áp dụng Đ. L. py-ta-go vào tg ABC vuông tạo A, có:
BC2=AC2+AB2.
=>BC2=82+62.
=64+36.
=100.
=>BC=10cm.
b, Vì góc BAC+ góc CAF=180o(kề bù)
=>góc CAF=180o-góc BAC
=180o-90o
=90o
Xét tg ABC và tg AFC, có:
AC chung
góc BAC= góc CAF(=90o)
AB=AF(gt)
=>tg ABC= tg AFC(c. g. c)
c, Vì tg ABC= tg AFC(cm câu b)
=>CF=CB(2 cạnh tương ứng)
=>tg CBF cân tại C.
d, Xét tg AHC và tg AKC, có:
góc HCA= góc KCA(2 góc tương ứng)
AC chung
góc AHC= góc AKC(2 góc tương ứng)
=>tg AHC= tg AKC(ch-gn)
=>CH=CK(2 cạnh tương ứng)
=>tg HKC cân tại C.
Ta có: tg HKC cân tại C, tg BFC cân tại C.
=> góc B= góc F= góc CHK= góc CKH.
Mà góc B và góc CHK ở vị trí đong vị, góc F và góc CKH cũng ở vị trí đồng vị.
=>BF//HK(đpcm)
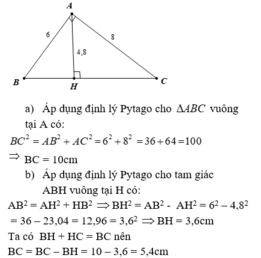
a: BC=10cm
b: BH=3,6cm
CH=6,4cm
làm hẳn ra từng bước hoojmik vs