P
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 4 2022
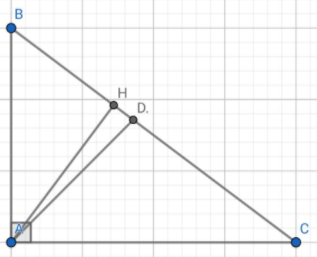
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
\(BH=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)
BR
5 tháng 12 2018
a)Vì AM là đường trung tuyền nên ta có
AM=1/2BC
AM=(1/2).5 => AM=2,5(cm)
b)áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có
AB^2+AC^2=BC^2
thay số ta có : 3^2+AC^2=5^2=>9+AC^2=25=>AC^2=25-9=16
=>AC= căn bậc 2 của 16
=>AC=4(cm)
diện tích tam giác ABC là:
S=1/2a.h=1/2.3.4=6(cm2)
Hết nhé ^_^
5 tháng 12 2018
ta có tam giác ABC vuông tại A
Áp dụng tỉ số lượng giác trong .........................
=> AM2=BM.BC
=>AM=\(\sqrt{2,5\times5}\approx3,6cm\)
diện tích tam giác vuông ABC là
STAM GIÁC ABC=\(\frac{1}{2}AM.BC=9cm^2\)
M
2
BT
30 tháng 12 2021
Bn ưi, giải thích ra cho mik nha, toán là cần giải thích vs đáp án nha, phiền bn giải thích ra cho mik.
9 tháng 4 2017
a AM.AB =AN.AC(=AH2)
b, AH=MN=2(do AMHN là hình chứ nhật)
tam giác AMN đồng dạng với ABC => tỉ số diện tích 2 tam giác là MN2/BC2=22/52=4/25
mà diện tích AMHN=2 lần diện tích AMN=> Diện tích AMHN =8/25 diện tích ABC
Tính được diện tích ABC => diện tích AMHN
29 tháng 8 2021
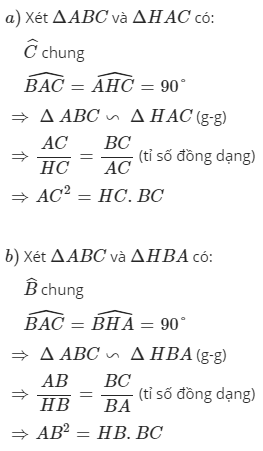
Mik copy trên mạng nên cs chút sai sót thì mog bn bỏ qua =)
29 tháng 8 2021
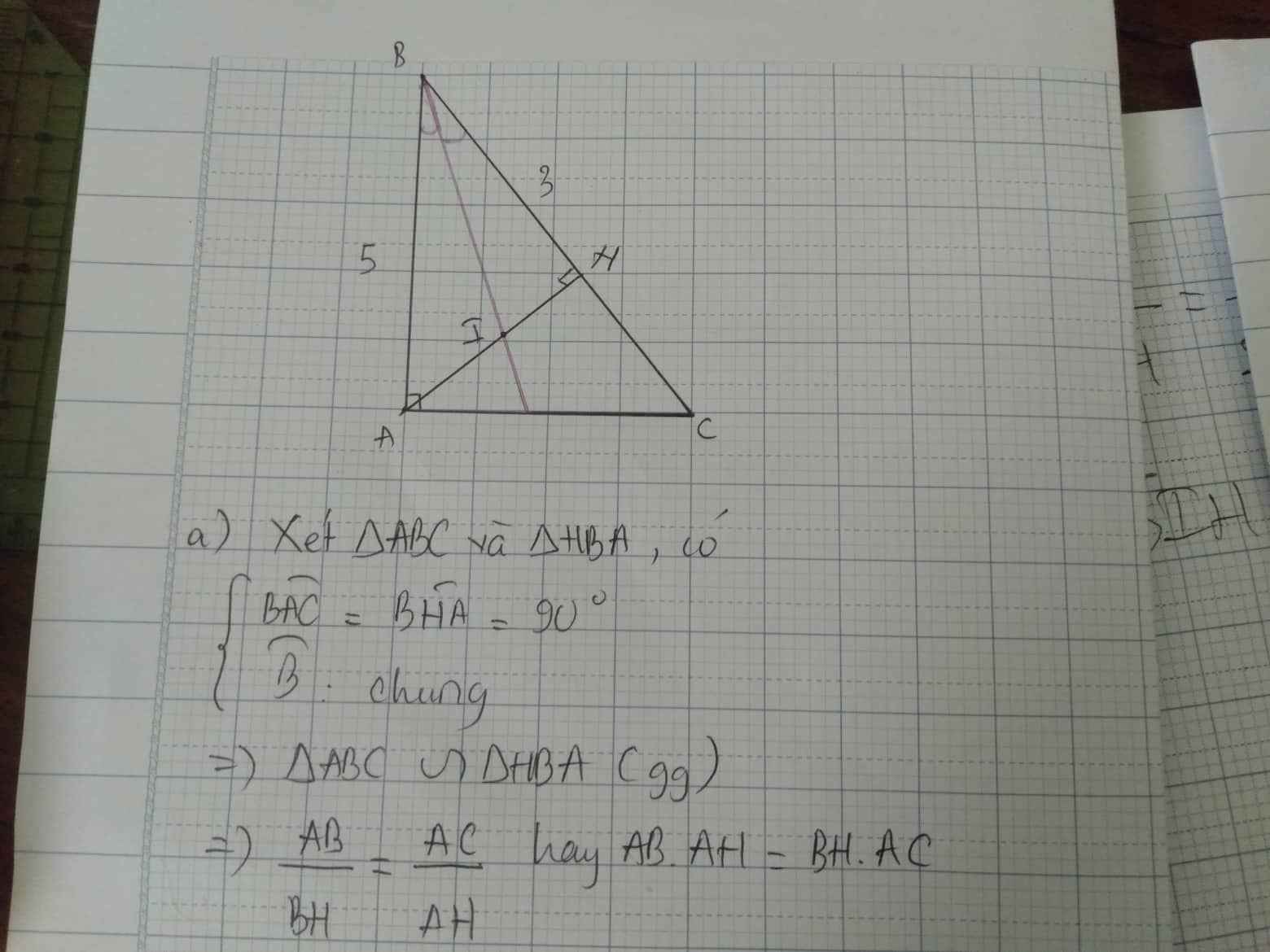
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=BH\cdot BC\)
17 tháng 3 2023
a: AD là phân giác
=>BD/AB=CD/AC
=>BD/6=3/9=1/3
=>BD=2cm
b: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot\left(2+3\right)=\dfrac{3}{2}\cdot5=\dfrac{15}{2}\left(cm^2\right)\)
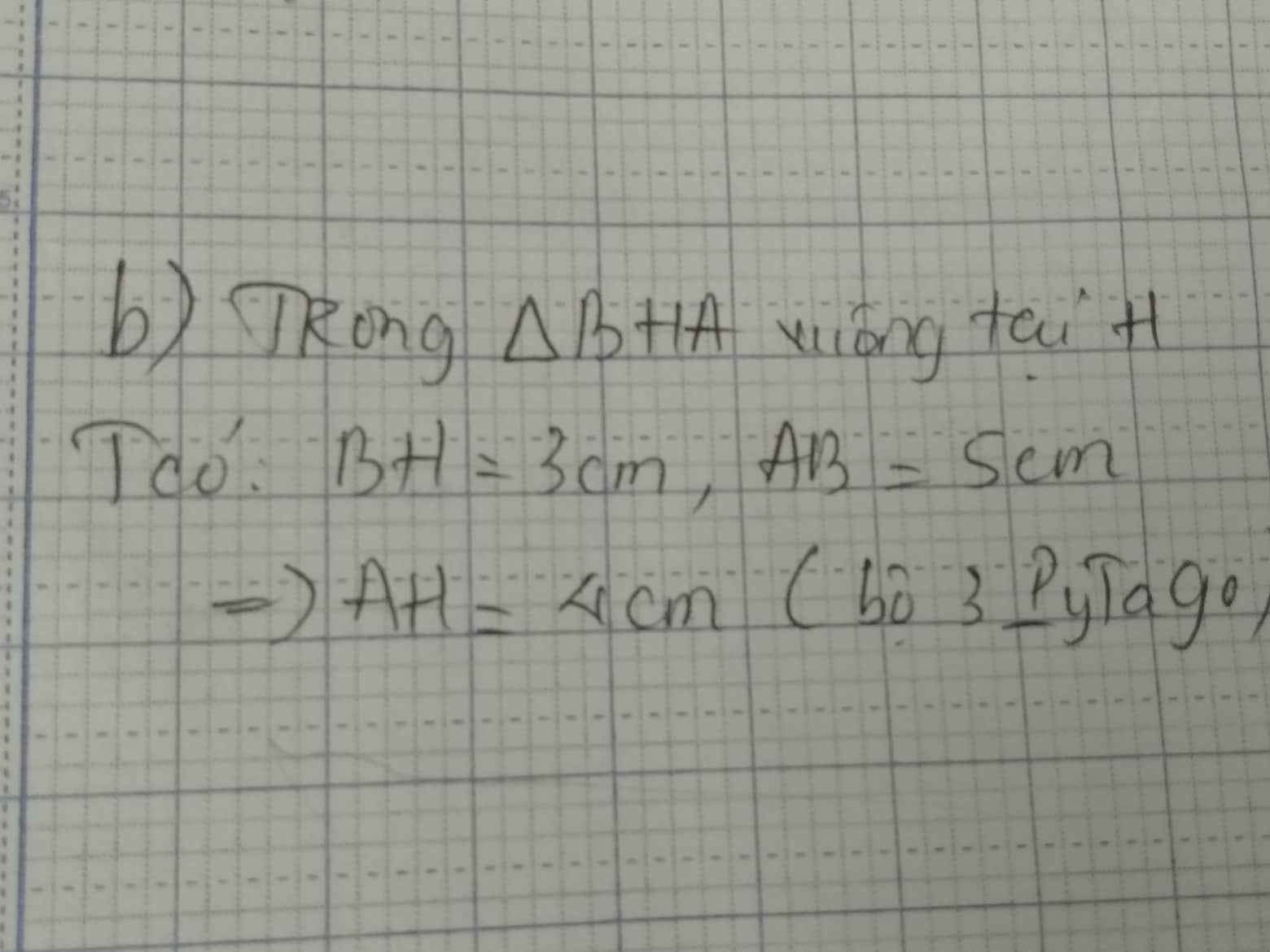
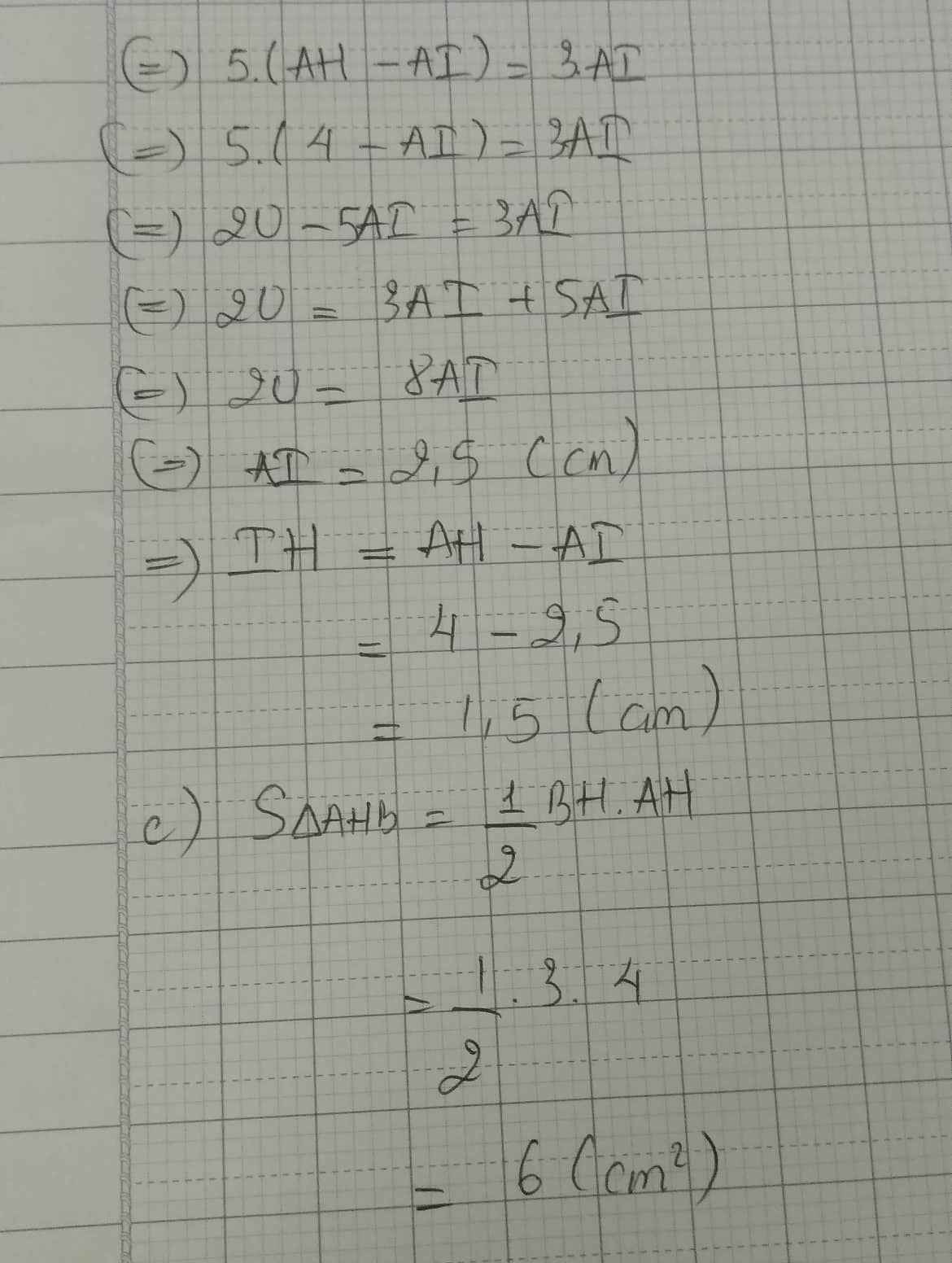
Xét \(\Delta ABC\)vuông tại A
=>AB2 +AC2=BC2
32+AC2=52=> AC2=52-32= 25-9=16
=> AC=\(\sqrt{16}\)=4
Diện tích \(\Delta ABC\) là: (ACxAB)/2=4x3/2=12/2=6(cm2)
Vậy: diện tích am giác ABC là 6 cm2
bạn dùng định lí pitago để tính cạnh AC nhé. AC=căn 34. sau khi có 3 cạnh thì tính diện tích