Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(4\sqrt{10}\right)^2-4^2=144\)
hay AB=12(cm)
Xét ΔABD vuông tại A có
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4}{12}=\dfrac{1}{3}\)
hay \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq36^052'\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{ABC}\)
\(\Leftrightarrow AC=12\cdot\tan36^052'\simeq9\)(cm)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot9}{2}=\dfrac{108}{2}=54\left(cm^2\right)\)

Theo t/c đường phân giác: AD/AB = ID/IB = 1/2 --> ID = 1/2AB
Mà AD² + AB² = BD² = 15².5 hay 1/4AB² + AB² = 15².5 --> AB = 30 --> AD = 15
Lại theo t/c đường phân giác: AD/DC = AB/BC --> DC/BC = AD/AB = 1/2
--> BC = 2DC
Theo đ/l Pytago AB² + AC² = BC² hay 30² + (DC + 15)² = 4DC²
<=> DC² - 10DC - 375= 0 --> DC = 25 (loại nghiệm -15)
--> AC = AD + DC = 15 + 25 = 40
--> S(ABC) = 1/2AB.AC = 35 cm²
Đọc dòng đầu thấy sai sai bạn ạ
AD/AB=ID/IB=1/2 =>ID=1/2 IB chứ ko phải AB

=) Áp dụng liên tục py-ta-go và định lí đường phân giác quá dễ đó bạn :V
\(\frac{AD}{AB}=\frac{ID}{IB}=\frac{1}{2}vs.AD^2+AB^2=\left(6\sqrt{3}+3\sqrt{3}\right)^2=...\\
\)
Tìm đ.c AD và AB
Làm tươn tự trên đối với tg ABC
\(\frac{AD}{DC}=\frac{AB}{BC}vs.AB^2+\left(AD+DC\right)^2=BC^2.\\
\)
\(Chỉ-cần-giải-hệ-là-ra-....\\
\)

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

Lời giải:
Theo tính chất tia phân giác:
$\frac{AB}{BC}=\frac{AD}{DC}=\frac{4\sqrt{10}}{5\sqrt{10}}=\frac{4}{5}$
$AC=4\sqrt{10}+5\sqrt{10}=9\sqrt{10}$
Áp dụng định lý Viet:
$BC^2=AB^2+AC^2$
$\Leftrightarrow (\frac{5}{4}AB)^2=AB^2+(9\sqrt{10})^2$
$\Leftrightarrow AB^2=1440$
$BD=\sqrt{AB^2+AD^2}=\sqrt{1440+(4\sqrt{10})^2}=\sqrt{1440+160}=40$ (cm)
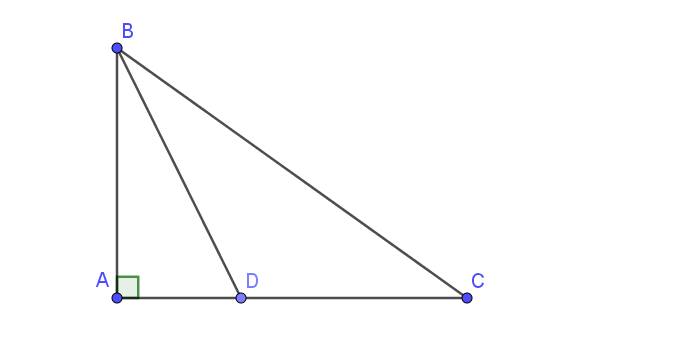
Đặt \(CD=x,BC=y\left(x,y>0\right)\)
Ta có \(AB=\sqrt{BD^2-AD^2}=12\)
Ta có hệ phương trình: \(\hept{\begin{cases}\frac{x}{y}=\frac{AD}{AB}=\frac{4}{12}=\frac{1}{3}\\12^2+\left(4+x\right)^2=y^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=3x\\144+\left(4+x\right)^2=\left(3x\right)^2\end{cases}}\Leftrightarrow\hept{\begin{cases}y=3x\\x=5\left(h\right)x=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=5\\y=15\end{cases}}\)(Vì \(x,y>0\))
Vậy \(S_{ABC}=\frac{AB.\left(AD+CD\right)}{2}=\frac{12.\left(4+5\right)}{2}=54.\)