Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xin lỗi. Chữ mình xấu.
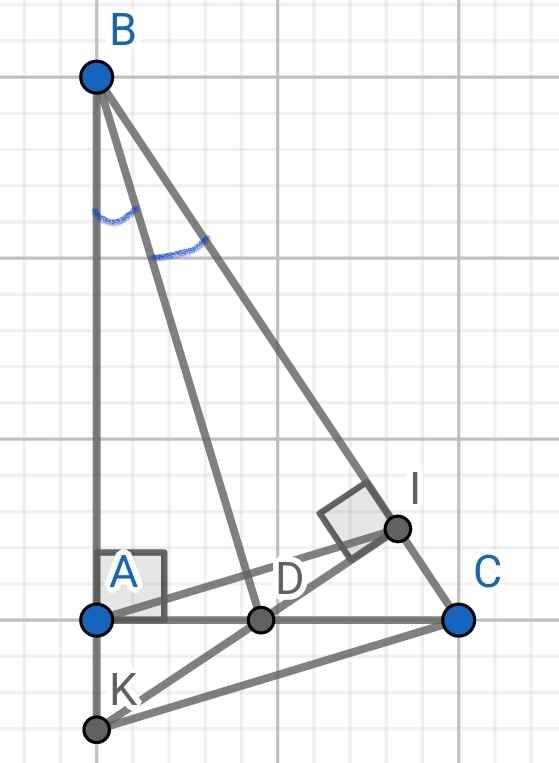
a) Xét hai tam giác vuông: ∆ABD và ∆IBD có:
BD chung
∠ABD = ∠IBD (gt)
⇒ ∆ABD = ∆IBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆IBD (cmt)
⇒ AD = ID (hai cạnh tương ứng)
∆DIC vuông tại I
⇒ DC là cạnh huyền
⇒ ID < DC
Mà AD = ID (cmt)
⇒ AD < DC
c) Xét hai tam giác vuông: ∆DAK và ∆DIC có:
AD = ID (cmt)
∠ADK = ∠IDC (đối đỉnh)
⇒ ∆DAK = ∆DIC (cạnh góc vuông - góc nhọn kề)
⇒ DK = DC (hai cạnh tương ứng)
d) Do ∆DAK = ∆DIC (cmt)
⇒ AK = IC (hai cạnh tương ứng)
Do ∆ABD = ∆IBD (cmt)
⇒ AB = IB (hai cạnh tương ứng)
∆ABI cân tại B
⇒ ∠BAI = ∠BIA = (180⁰ - ∠ABC)/2 (1)
Do AB = IB (cmt)
AK = IC (cmt)
⇒ BK = BC
⇒ ∆BCK cân tại B
⇒ ∠BKC = ∠BCK = (180⁰ - ∠ABC)/2 (2)
Từ (1) và (2) ⇒ ∠BAI = ∠BKC
Mà ∠BAI và ∠BKC là hai góc đồng vị
⇒ AI // KC
A B C I D K E H
a)Xét \(\Delta ABD=\Delta IBD\left(ch-gn\right)\Rightarrow AB=BI;AD=DI.\)
b)Xét \(\Delta ABH=\Delta IBH\left(c-g-c\right)\Rightarrow AHB=IHB=90^0\)
Suy ra \(AI\perp BD\)
c)XÉT \(\Delta ADK=\Delta IDC\left(cgv-gnk\right)\Rightarrow KB=DC\)
d) vì \(BD//EI\Rightarrow DBI=BIE;DBI=BEI\)
HAY \(BIE=BEI\Rightarrow\Delta BIE\)CÂN TẠI B
a: Sửa đề: AB=6cm
BC=căn 6^2+8^2=10cm
b: Xét ΔABD vuông tại A và ΔIBD vuông tại I có
BD chung
góc ABD=góc IBD
=>ΔBAD=ΔBID
c: ΔBAD=ΔBID
=>BA=BI
=>ΔBAI cân tại B
d: BA=BI
DA=DI
=>BD là trung trực của AI
f: AD=DI
DI<DC
=>AD<DC
g: Xét ΔBIK vuông tại I và ΔBAC vuông tại A có
BI=BA
góc IBK chung
=>ΔBIK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
Tự vẽ hình.
a) Xét \(\Delta\)ABD vuông tại A và \(\Delta\)IBD vuông tại I có:
BD chung
\(\widehat{ABD}\) = \(\widehat{IBD}\) (BD là tia pg)
=> \(\Delta\)ABD = \(\Delta\)IBD (ch - gn)
b) Gọi giao điểm của AI và BD là E.
Vì \(\Delta\)ABD = \(\Delta\)IBD (câu a)
=> AB = IB (2 cạnh t/ư) và AD = ID(2 cạnh t/ư)
Xét \(\Delta\)ABE và \(\Delta\)IBE có:
AB = IB (c/m trên)
\(\widehat{ABE}\) = \(\widehat{IBE}\) (suy từ gt)
BE chug
=> \(\Delta\)ABE = \(\Delta\)IBE (c.g.c)
=> \(\widehat{AEB}\) = \(\widehat{IEB}\) (2 góc t/ư)
mà \(\widehat{AEB}\) + \(\widehat{IEB}\) = 180o (kề bù)
=> \(\widehat{AEB}\) = \(\widehat{IEB}\) = 90o
Do đó BD \(\perp\) AI.
c) Xét \(\Delta\)IDC và \(\Delta\)ADK có:
\(\widehat{CID}\) = \(\widehat{KAD}\) (=90O)
ID = AD (câu b)
\(\widehat{IDC}\) = \(\widehat{ADK}\) (đối đỉnh)
=> \(\Delta\)IDC = \(\Delta\)ADK (g.c.g)
=> DC = DK (2 cạnh t/ư)
cam on nha