Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
1.
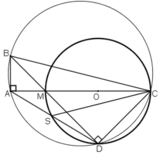
$\widehat{MDC}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{BDC}=90^0$
Tứ giác $ABCD$ có $\widehat{BAC}=\widehat{BDC}=90^0$ và cùng nhìn cạnh $BC$ nên là tgnt.
Do $ABCD$ nội tiếp nên $\widehat{BCA}=\widehat{BDA}$
Mà $\widehat{BDA}=\widehat{MCS}$ (do $MDSC$ nội tiếp)
$\Rightarrow \widehat{BCA}=\widehat{MCS}$
$\Rightarrow CA$ là phân giác $\widehat{BCS}$
2.
Gọi $T$ là giao điểm của $BA$ và $EM$
Xét tam giác $BTC$ có $TE\perp BC$ (do $\widehat{MEC}=90^0$) và $CA\perp BT$ và $TE, CA$ giao nhau tại $M$ nên $M$ là trực tâm tam giác $BTC$
$\Rightarrow BM\perp TC$.
Mà $BM\perp DC$ nên $TC\parallel DC$ hay $T,D,C$ thẳng hàng
Do đó $BA, EM, DC$ đồng quy tại $T$
3.
Vì $ABCD$ nt nên $\widehat{MAD}=\widehat{CAD}=\widehat{DBC}=\widehat{MBE}$
Dễ cm $BAME$ nội tiếp cho $\widehat{A}+\widehat{E}=90^0+90^0=180^0$ nên $\widehat{MBE}=\widehat{EAM}$
Do đó: $\widehat{MAD}=\widehat{EAM}$ nên $AM$ là tia phân giác $\widehat{EAM}(*)$
Mặt khác:
Cũng do $MECD,ABCD$ nội tiếp nên:
$\widehat{ADM}=\widehat{ADB}=\widehat{ACB}=\widehat{MCE}=\widehat{MDE}$
$\Rightarrow DM$ là tia phân giác $\widehat{ADE}(**)$
Từ $(*); (**)\Rightarrow M$ là tâm đường tròn nội tiếp $ADE$.
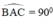⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
a: góc CDM=1/2*sđ cung CM=90 độ
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
c: Gọi F là giao của AB và CD
góc MEC=1/2*sđ cung MC=90 độ
=>ME vuông góc CB(1)
Xet ΔFCB có
CA,BD là đường cao
CA cắt BD tại M
=>M là trực tâm
=>FM vuông góc BC(2)
Từ (1), (2) suy ra F,M,E thẳng hàng
a,ta có góc MAB=90°; MNB=90°(gt);(góc nội tiếp chắn 1/2đtròn)
xét tứ giác AMNB có góc MAN+MNB=90°+90°=180°
suy ra AMNB nội tiếp
b, ta có góc CAB=90°(gt); CPB=90°( góc nội tiếp chắn 1/2đtròn)
xét tứ giác CPAB có góc CAB=CPB=90°
suy ra CPAB nội tiếp ( hai góc bằng nhau cùng chắn cung CB)
suy ra góc BCA=BPA(1)
góc PBA=PCA(2)
mà góc MPN=ACB=1/2sđcung MN(3)
góc PCA=PNM=1/2sđcung PM(4)
từ 1,3 suy ra góc ACB=MPN
từ 2,4 suy ra góc PNM=PBA
xét hai tam giác PAB và PMN có
góc APB=MPN(cmt)
góc PNM=PBA(cmt)
suy ra hai tam giác đó đồng dạng (đpcm)
c, ta có góc PDN=PCN=1/2sđ cung PN(1)
góc PAC=PBC(CPAB nội tiếp)(2)
mà góc PBC+PCB=90°(3)
từ 1,2,3 suy ra góc DAC+ADE=90°
suy ra DN vuông với AC
xét hai tam giác PCM và ECG có góc C chung
góc CEG=CPM=90°
suy ra hai tam giác đó đồng dạng
suy ra PC/EC=CM/CG
suy ra PC.CG=EC.CM(đpcm)
a) Dễ thấy tứ giác AMNC nội tiếp đường tròn đường kính MN.
b) Ta có tứ giác AMNC nội tiếp nên \(\angle BCM=\angle BAN\). Suy ra \(\Delta BCM\sim\Delta BAN\left(g.g\right)\).
Từ đó \(\dfrac{BM}{BN}=\dfrac{CM}{AN}\).
c) Gọi P' là trung điểm của MC.
Khi đó P' là tâm của đường tròn ngoại tiếp tứ giác AMNC.
Ta có \(\widehat{AP'N}=2\widehat{ACN}=180^o-2\widehat{ABC}=180^o-\widehat{MON}\). Suy ra tứ giác AONP' nội tiếp.
Từ đó \(P'\equiv P\). Ta có \(OP=OP'=\dfrac{BC}{2}\) (đường trung bình trong tam giác BMC) không đổi khi M di động trên cạnh AB.
