K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

L
14 tháng 12 2021
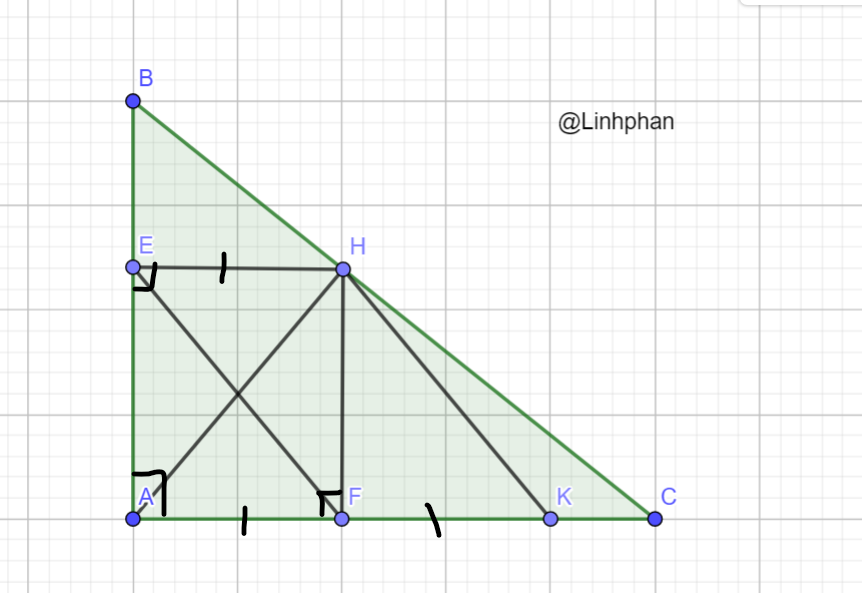
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)
a, Xét tứ giác AEHF có : ^AEH = ^EAF = ^HFA = 900
Vậy tứ giác AEHF là hcn
=> AH = EF ( 2 đường chéo bằng nhau )
c, Theo Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=3cm\)
SABC = 1/2 . AB . AC = 1/2 . 3 . 4 = 6 cm2
a) Xét tứ giác AEHF:
\(\widehat{EAF}=90^o;\widehat{AEH}=90^o;\widehat{AFH}=90^o\)
(Do tam giác ABC vuông tại A; HE và HF lần lượt vuông góc với AB và AC).
=> AEHF là hình chữ nhật (dhnb).
=> AH = EF (Tính chất 2 đường chéo của hình chữ nhật).
b) Ta có: FK = AF (gt).
Mà AF = EH (AEHF là hình chữ nhật).
=> AF = EH = FK.
Ta có: EH // AF (AEHF là hình chữ nhật).
Mà F thuộc AK (gt).
=> EH // FK.
Xét tứ giác EHKF:
EH // FK (cmt).
EH = FK (cmt).
=> EHKF là hình bình hành (dhnb).
c) Xét tam giác ABC vuông tại A:
Ta có: BC2 = AB2 + AC2 (Định lý Pytago).
Thay số: 52 = AB2 + 42.
=> AB2 = 9. => AB = 3.
Diện tích tam giác ABC vuông tại A:
\(\dfrac{1}{2}AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right).\)