BN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
7 tháng 10 2021
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay \(BC=\sqrt{193}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{\sqrt{193}}\)
\(\Leftrightarrow\widehat{B}\simeq60^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
T
10 tháng 9 2018
a)\(12^2+16^2=20^2\)(144+256=400)
\(\Rightarrow AB^2+AC^2=BC^2\)(định lý pytago)
\(\Rightarrow\Delta ABC\)vuông tại A
b)Xét tg ABC vuông tại A có đcao AH(cmt)
Ta có:AB.AC=BC.AH(Hệ thức lượng)
12.16=20.AH
192=20.AH
AH=192:20=9.6
c)cosB=AB/BC,cosC=AC/BC
\(\Rightarrow\frac{AB.AB}{BC}+\frac{AC.AC}{BC}\)
\(\Rightarrow\frac{AB^2}{BC}+\frac{AC^2}{BC}=\frac{\left(AB^2+AC^2\right)}{BC}\)
\(\Rightarrow\frac{BC^2}{BC}=\frac{20^2}{20}=20\)
\(\Rightarrow AB.cosB+AC.cosC=20\)
CM
24 tháng 3 2019
a, Sử dụng tỉ số cosC và sinC, tính được
a = 20 3 3 cm, c = 10 3 3 cm và B ^ = 60 0
b, Sử dụng tỉ số sinB và cosB, tính được:
b = 20.sin 35 0 ≈ 11,47cm, c = 20.cos 35 0 ≈ 16,38cm
c, Sử dụng định lý Pytago và tỉ số sinB, tính được:
c = 5 5 cm, sinB = 10 15 => B ^ ≈ 41 , 8 0 , C ^ ≈ 48 , 2 0
d, Tương tự c) ta có
a = 193 cm, tanB = 12 7 => B ^ ≈ 59 , 7 0 , C ^ = 30 , 3 0
CM
5 tháng 7 2019
Áp dụng định lý Pytago cho vuông tại A có:
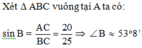
Đáp án cần chọn là: B
BN
1
H9
HT.Phong (9A5)
CTVHS
16 tháng 9 2023
Xét tam giác ABC vuông tại A ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BH\cdot BC=AB^2\\HC\cdot BC=AC^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7,2\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{16^2}{20}=12,8\left(cm\right)\end{matrix}\right.\)
12 tháng 7 2023
1:
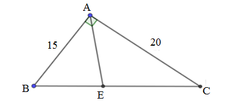
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm
Áp dụng định lý Py-ta-go vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Mà: \(sinB=\dfrac{AC}{BC}=\dfrac{16}{20}\)
\(\Rightarrow sinB=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-53^o\approx37^o\)