Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét ΔADC vuông tại D và ΔBEC vuông tại E có
\(\widehat{C}\) chung
Do đó: ΔADC\(\sim\)ΔBEC

Bài 2:
a: \(\sin\alpha=\sqrt{1-\left(\dfrac{2}{5}\right)^2}=\dfrac{\sqrt{21}}{5}\)
\(\tan\alpha=\dfrac{\sqrt{21}}{5}:\dfrac{2}{5}=\dfrac{\sqrt{21}}{2}\)
\(\cot\alpha=\dfrac{2}{\sqrt{21}}=\dfrac{2\sqrt{21}}{21}\)
b: Đặt \(\cos\alpha=a;\sin\alpha=b\)
Theo đề, ta có: a-b=1/5
=>a=b+1/5
Ta có: \(a^2+b^2=1\)
\(\Leftrightarrow b^2+\dfrac{2}{5}b+\dfrac{1}{25}+b^2-1=0\)
\(\Leftrightarrow2b^2+\dfrac{2}{5}b-\dfrac{24}{25}=0\)
\(\Leftrightarrow10b^2+2b-24=0\)
=>b=4/5
=>a=3/5
\(\cot\alpha=\dfrac{a}{b}=\dfrac{3}{4}\)

Góc 2α = A M H ^
a, Ta có: sin 2 α = A H A M = 2 A H A M = 2 A B . A C B C 2 = 2 sin α . cos α
b, 1 + cos2α = 1 + H M A M = H C A M = 2 H C B C = 2 . A C 2 B C 2 = 2 cos 2 α
c, 1 – cos2α = 1 - H M A M = H B A M = 2 H B B C = 2 . A B 2 B C 2 = 2 sin 2 α

D = \(\left(sin^2a+cos^2a\right)+\left(cos\left(90-a\right)-sina\right)+1+\left(tan^2\left(90-a\right)-\frac{1}{sin^2a}\right)\)
\(=1+\left(sina-sina\right)+1+\left(cot^2a-1-cos^2a\right)=1+1-1=1\)
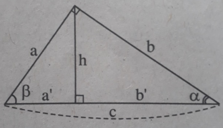
a: sin a=sin C=AB/BC
cos a=AC/BC=b/a
sin 2a=2sinacosa\(=2\cdot\dfrac{b}{a}\cdot\dfrac{AB}{BC}=\dfrac{2b\cdot AB}{a^2}\)
b: \(sin2a=sin\left(a+a\right)\)
\(=sina\cdot cosa+sina\cdot cosa\)
\(=2\cdot sina\cdot cosa\)