Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!

mình chỉ giúp ý d theo mong muốn của bạn thôi :)
Có : AH = AK ( cái này bạn chứng minh ở câu trên chưa mình không biết; nếu chưa thì bạn chứng minh đi nhé )
=> A thuộc đường trung trực của HK
và MH=MK
=> M thuộc đường trung trực của HK
=> AM là đường trung tực của HK
=> AM ⊥ HK

K
Hình hơi xấu hì hì! tự viết GT KL nha!
Cm:
a) \(\Delta ABC\)cân tại A (gt)
=> AB=AC
=>AC=4cm (vì AB=4cm(gt))
Vậy AC=4cm.
b) \(\Delta ABC\)cân tại A (gt)
=>\(\widehat{B}=\widehat{C}\)
\(\Delta ABC\)có:\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(ĐL tổng 3 góc trong 1 tam giác)
\(\Rightarrow60^0+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=60^0\)
=> \(\Delta ABC\)đều.
c) Xét \(\Delta ABM\)và \(\Delta ACM\)có:
AM chung
AB=AC
BM=CM
=>\(\Delta ABM\)=\(\Delta ACM\) (c.c.c)
(đpcm)
d) Vì \(\Delta ABM\)=\(\Delta ACM\)(cmt)
=>\(\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(2 góc kề bù)
=>\(\widehat{AMB}=\widehat{AMC}=90^0\)
=> \(AM⊥BC\)(Đpcm)
e)Xét \(\Delta BHM\)và \(\Delta CKM\)có:
\(\widehat{BHM}=\widehat{CKM}=90^0\)
BM=CM
\(\widehat{B}=\widehat{C}\)
=>\(\Delta BHM\)=\(\Delta CKM\)(cạnh huyền-góc nhọn)
=>MH=MK(2 cạnh t/ứ)
(đpcm)

A B C M 4cm H K
a)Ta có: tam giác ABC là tam giác cân
\(=>AB=AC\)
Mà \(AB=4cm\)
=>>AC=4cm
b) Nếu góc B=60 độ =>tgiác ABC là tam giác đèu(t/c)
c) Xét tam giác ABM và tgiác ACM có
AB=AC(cmt)
AM: chung
==>>tgiác ABM=tgiác ACM( ch-cgv)
d) Ta có: tam giác ABM=tgiác ACM(cmt)
=>\(\widehat{AMC}=\widehat{AMB}\)(2 góc tương ứng)
Mà: \(\widehat{AMC+}\widehat{AMC}=180^0\)
\(=>\widehat{AMC=}\widehat{AMB}=\frac{180^0}{2}=90^0\)
=> AMvuông góc vs BC
e) Xét tgiác BMH và tgiác CMK có :
BM=CM( 2 cạnh tương ứng , cmt(a))
\(\widehat{B}=\widehat{C}\)( tgiác ABC là tgiác đều)
==>>>tgiác BMH=tgiác CMK(ch-gn)
=>MH=MK( 2 cạnh tương ứng)

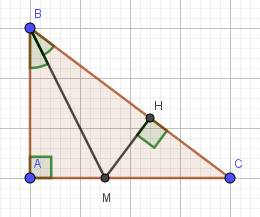
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)

a, bởi vi AH là trung tuyến của góc A và cắt BC tại M nên suy ra AM=1/2BC cho nên suy ra AM=MC cho nên suy ra tam giac AMH= tam giac MHC
b,phai. theo câu a ta có tam giac MAC là tam giác cân . mà theo định lí traong tam giac cân đường cao cũng đong thời là đường phan giác cho neen suy ra MH là đường phân giác góc M
c,tam giac AMB là tam giac cân vi chung minh tuong yu theo câu a ta co AM=BM