Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE

Tham khảo:
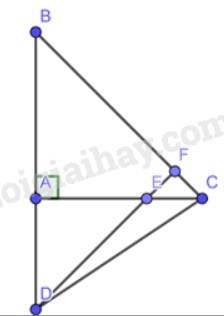
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC

a)xét tam giác ABM và tam giác DCM có:
BN=CM(GT)
góc BMA=góc CMD(đđ)
AM-DM(GT)
\(\Rightarrow\)tam giác ABM=tam giác DCM(c.g.c)
b)theo câu a: tam giác ABM=tam giác DCM
\(\Rightarrow\)góc BAM= góc MDC(2 góc tương ứng)
mà đây là cặp góc so le trong
\(\Rightarrow\)AB//CD
\(\Rightarrow\)góc BAC= góc ACD=90 độ\(\Rightarrow\)CD \(\perp\)AC
c) xét tam giác AHC và tam giác EHC có:
AH=EH(GT)
góc AHC=góc EHC=90 độ
HC chung
\(\Rightarrow\)tam giác AHC = tam giác EHC(c.g.c)
\(\Rightarrow\)CA=CE(2 cạnh tương ứng)
\(\Rightarrow\)tam giác CAE cân tại C

a) Có : \(\widehat{ABC}+\widehat{ABD}=\widehat{ACB}+\widehat{ACE}=180^o\)
Mà : \(\widehat{ABC}=\widehat{ACB}\)(tam giác ABC cân tại A)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\)
-Xét tam giác ABD và ACE có :
AB=AC (tam giác ABC cân tại A)
BD=CE(đều bằng AB)
\(\widehat{ABD}=\widehat{ACE}\left(cmt\right)\)
=> Tam giác ABD=ACE(c.g.c)
=> AD=AE
=> Tam giác ADE cân tại A(đccm)
b) Tam giác ABC cân tại A có : \(\widehat{BAC}=40^o\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-40^o}{2}=70^o\)
- Có : \(\widehat{ABC}+\widehat{ABD}=180^o\)
\(\Rightarrow70^o+\widehat{ABD}=180^o\)
\(\Rightarrow\widehat{ABD}=110^o\)
- Xét tam giác ABD cân tại B(BD=AB) có :
\(\widehat{ABD}+\widehat{BAD}+\widehat{ ADB}=180^o\)
\(\Rightarrow110^o+\widehat{BAD}+\widehat{ADB}=180^o\)
\(\Rightarrow\widehat{BAD}=\widehat{BDA}=\frac{180^o-110^o}{2}=35^o\)
- Tương tự, ta có : \(\widehat{AEC}=\widehat{CAE}=35^o\)
- Có : \(\widehat{DAE}=\widehat{DAB} +\widehat{CAE}+\widehat{BAC}=35^o+35^o+40^o=110^o\)
Vậy : \(\widehat{D}=\widehat{E}=35^o,\widehat{DAE}=110^o\)
c) Tam giác ABD cân tại B(AB=BD) có \(BH\perp DA\)
=> HD=HA(t/c đg TT,PG,cao,.. của tam giác cân)
Tương tự có AK=KE
Mà : AD=AE(tam giác ADE cân tại A)
=> AH=AK
-Xét tam giác AHO và AKO, có :
AH=AK(cmt)
\(\widehat{AHO}=\widehat{AKO}=90^o\)
AO-cạnh chung
=> Tam giác AHO=AKO(cạnh huyền-cạnh góc vuông)
=> HO=OK(đccm)
d) Do tam giác AHO=AKO(cmt)
=> \(\widehat{HAO}=\widehat{KAO}\)
\(\Rightarrow\widehat{HAB}+\widehat{BAO}=\widehat{KAC}+\widehat{CAO}\)
Mà : \(\widehat{HAB}=\widehat{KAC}=35^o\left(cmt\right)\)
Mà :\(\widehat{BAO}+\widehat{CAO}=\widehat{BAC}\)
\(\Rightarrow\widehat{BAO}=\widehat{CAO}=\frac{\widehat{BAC}}{2}=\frac{40}{2}=20^o\)
- Gọi giao điểm của AO và BC là I
Xét tam giác AIB có : \(\widehat{BAI}+\widehat{ABI}+\widehat{AIB}=180^o\)
\(\Rightarrow20^o+70^o+\widehat{AIB}=180^o\)
\(\Rightarrow90^o+\widehat{AIB}=180^o\)
\(\Rightarrow\widehat{AIB}=90^o\)
\(\Rightarrow AI\perp BC\left(đccm\right)\)
#H
gọi K là giao của ED và BC
ΔAED vuông tại A có AD=AE
nên ΔAED vuông cân tại A
góc KCE+góc KEC=45+45=90 độ
=>ED vuông góc BC