Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Từ giả thiết ta có:
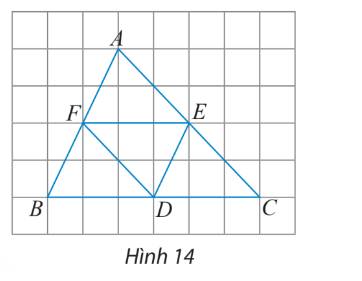
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

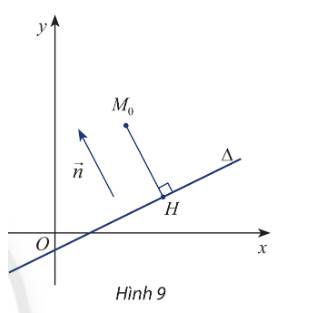
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)

A B C H M
Có \(\overrightarrow{MH}=-\overrightarrow{HM}=\dfrac{-1}{2}\left(\overrightarrow{HB}+\overrightarrow{HC}\right)\);
\(\overrightarrow{MA}=-\overrightarrow{AM}=\dfrac{-1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\).
Vì vậy:
\(\overrightarrow{MH}.\overrightarrow{MA}=\dfrac{-1}{2}\left(\overrightarrow{HB}+\overrightarrow{HC}\right).\dfrac{-1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\left(\overrightarrow{HB}.\overrightarrow{AB}+\overrightarrow{HB}.\overrightarrow{AC}+\overrightarrow{HC}.\overrightarrow{AB}+\overrightarrow{HC}.\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\left(\overrightarrow{CH}.\overrightarrow{AC}+\overrightarrow{BH}.\overrightarrow{AB}\right)\) (Do H là trực tâm tam giác ABC).
\(=\dfrac{1}{4}\left[\overrightarrow{CH}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{BH}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\right]\)
\(=\dfrac{1}{4}\left(\overrightarrow{CH}.\overrightarrow{AB}+\overrightarrow{CH}.\overrightarrow{BC}+\overrightarrow{BH}.\overrightarrow{AB}+\overrightarrow{BH}.\overrightarrow{BC}\right)\)
\(=\dfrac{1}{4}\left(\overrightarrow{CH}.\overrightarrow{BC}+\overrightarrow{BH}.\overrightarrow{BC}\right)\) ( do H là trực tâm tam giác ABC).
\(=\dfrac{1}{4}\overrightarrow{BC}\left(\overrightarrow{BH}+\overrightarrow{HC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{BC}.\overrightarrow{BC}=\dfrac{1}{4}BC^2\).

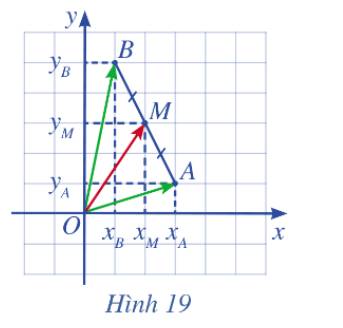
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
C = (-4.1, -6.64)
C = (-4.1, -6.64)
C = (-4.1, -6.64)
D = (11.26, -6.64)
D = (11.26, -6.64)
D = (11.26, -6.64)
E = (-4.34, -6.06)
E = (-4.34, -6.06)
E = (-4.34, -6.06)
F = (11.02, -6.06)
F = (11.02, -6.06)
F = (11.02, -6.06)
Có \(BH\perp AC\). (1)
\(\widehat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn) vì vậy\(AC\perp DC\). (2)
Từ (1) và (2) suy ra BH//DC. (3)
Tương tự HC//BD (vì cùng vuông góc với AB). (4)
Từ (3);(4) suy ra tứ giác HCDB là hình bình hành.
b) Do O là trung điểm của AD nên \(\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO}\).
Do M là trung điểm của BC nên \(\overrightarrow{HB}+\overrightarrow{HC}=2\overrightarrow{HM}=\overrightarrow{HD}\).
Vì vậy \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO}\).
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OH}+\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}\)
\(=3\overrightarrow{HO}+2\overrightarrow{HO}=2\left(\overrightarrow{HO}+\overrightarrow{OH}\right)+\overrightarrow{HO}\)
\(=2.\overrightarrow{0}+\overrightarrow{HO}=\overrightarrow{HO}\).
c) Ta có:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)\(=3\overrightarrow{OG}\) (theo tính chất trọng tâm tam giác). (5)
Mặt khác theo câu b)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\). (6)
Theo (5) và (6) ta có: \(\overrightarrow{OH}=3\overrightarrow{OG}\).
Suy ra ba điểm O, H, G thẳng hàng ( đường thẳng Ơ-le).
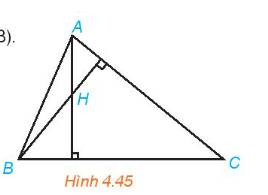

a) \( AH \bot BC\) và \(BH \bot CA\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \)
Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
b) Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH} = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)
Ta có: \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BC} = (8 - 8;8 - ( - 1)) = (0;9)\)
\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)
Lại có: \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \) và \(\overrightarrow {CA} = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)
\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)
Vậy H có tọa độ (6; 2)
c) Ta có: \(\overrightarrow {AB} = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}} = 3\sqrt {10} \)
Và \(\overrightarrow {BC} = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}} = 9\);
\(\overrightarrow {CA} = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}} = 3\sqrt {13} .\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)
\( \Rightarrow \widehat C \approx 56,{31^o}\)
Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)