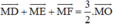Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

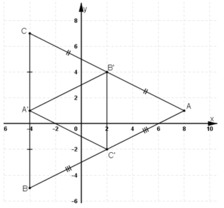
A’ là trung điểm của BC 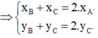
B’ là trung điểm của AC 
C’ là trung điểm của BA 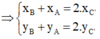
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
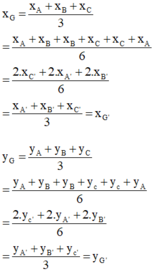
Vậy G ≡ G’ (đpcm)

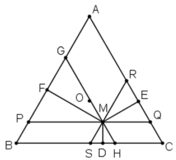
Ta có:
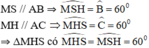
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
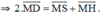
Chứng minh tương tự ta có:
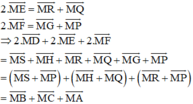
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
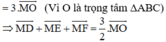

A B C A' B' C' a)Do A',B',C' là trung điểm BC,CA,AB=> A'B' song song với AB,B'C'song song với BC,C'A' song song với CA
\(\overrightarrow{A'B'}=\left(6;3\right)\) => VTPT của đường thẳng AB là: \(\overrightarrow{n}=\left(1;-2\right)\)
và C' thuộc (AB)=>Phương trình đường thẳng AB là:
(AB): x-2y-6=0
Tương tự ta có phương trình đường thẳng BC là:
(BC): x+4=0
Tọa độ điểm B là nghiệm hệ
\(\left\{{}\begin{matrix}\text{x-2y-6=0}\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-5\end{matrix}\right.\)
=>B(-4;-5)
A'(-4;1) là TĐ của BC => tọa độ C(-4;7)
C'(2;-2) là TĐ của AB =>tọa độ A(8;1)
b) Gọi tọa độ trọng tâm G của tam giác A'B'C' là G(x;y)
=>\(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=0\)
=>\(\left\{{}\begin{matrix}\left(-4-x\right)+\left(2-x\right)+\left(2-x\right)=0\\\left(1-y\right)+\left(4-y\right)+\left(-2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
=>G(0;1)
Thay vào tính
Ta có:\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\) =(8-4-4;1-1+7-1-5-1)=(0;0)
=>G là trọng tâm tam giác ABC=>ĐPCM

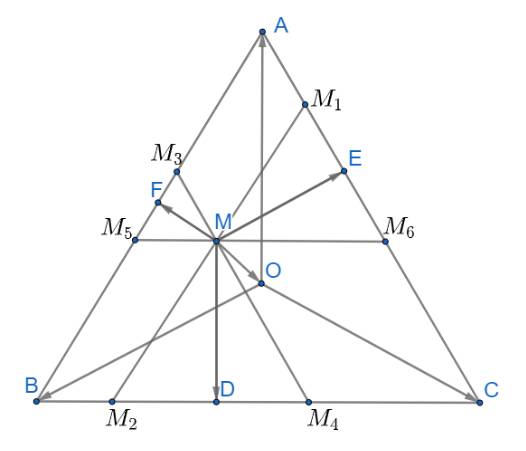
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)