Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔADB và ΔAEC có:
AB=AC(gt)
A: chung
AD=AE(gt)
=>ΔADB=ΔAEC(c.g.c)
=>đpcm
b) Có: AB=AC
=>ΔABC cân ở A
=>ABC=ACB(t/c Δ cân)
=>ABD+DBC=ACE+ECB
Mà ABD=ACE(ΔADB=ΔAEC)
=>DBC=ECB
=>ΔBCF cân ở F
=>BF=CF(t/c Δ cân)
c) Ta có:
AB=AE+EB
AC=AD+DC
Mà AB=AC; AE=AD
=>EB=DC
Xét ΔEBC và ΔDCB có:
EB=DC(cmt)
EBC=DCB(ΔABC cân)
BC: chung
=>ΔEBC=ΔDCB(c.g.c)
=>CEB=BDC(hai cạnh tương ứng)
Mà AEC+BEC=ADB+CDB=180°
=>AEC=ADB
Ta có:
EC=EF+FC
BD=BF+FD
Mà EC=BD(ΔEBC=ΔDCB); BF=CF(cmt)
=>FE=FD
Xét ΔAFE và ΔAFD có:
AE=AD(gt)
AEF=ADF(cmt)
FE=FD(cmt)
=>ΔAFE=ΔAFD(c.g.c)
=>EAF=DAF(hai góc tương ứng)
=>AF là pg BAC(1)
Xét ΔHAB và ΔHAC có:
ABH=ACHF(ΔABC cân)
HB=HC(H là trđ BC)
BAH=CAH(cmt)
=>ΔHAB=ΔHAC(g.c.g)
=>BAH=CAH(hai góc tương ứng)
=>AH là pg BAC(2)
Từ (1) và (2)
=>A, F, H thuộc thẳng hàng

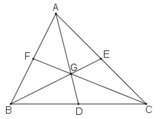
Trên đường trung tuyến AD có điểm G thỏa mãn: 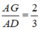
Suy ra: G là trọng tâm tam giác ABC.
Do tia BG cắt AC tại E nên E là trung điểm của AC.
Do tia CG cắt AB tại F nên F là trung điểm của AB.
Theo tính chất trọng tâm tam giác ta có:
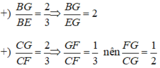
Chọn (B)

A B C M F E G
xét \(\Delta BME\)và\(\Delta CMA\)có \(\hept{\begin{cases}BM=MC\left(gt\right)\\\widehat{BME}=\widehat{CMA}\\ME=MA\left(gt\right)\end{cases}}\)(đối đỉnh)
do đó tam giác BME= tam giác CME (c.g.c)
suy ra BE = AC ( 2 cạnh tương ứng )
và \(\Rightarrow\widehat{EBM}=\widehat{ACM}\)( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong suy ra BE//AC
suy ra \(\widehat{BAC}=\widehat{EBA}\)( đồng vị )
xét \(\Delta FBE\)và \(\Delta BAC\)có \(\hept{\begin{cases}FB=BA\left(gt\right)\\\widehat{FBE}=\widehat{BAC}\left(cmt\right)\\BE=AC\left(cmt\right)\end{cases}}\)
do đó \(\Delta FBE=\Delta BAC\left(c.g.c\right)\)
suy ra \(\widehat{BFE}=\widehat{ABC}\) mà 2 góc này ở vị trí đồng vị nên BC//FE (1)
chứng minh tương tự ta có \(\Delta EMC=\Delta AMB\left(c.g.c\right)\)\(\Rightarrow AB=EC\)( 2 cạnh tương ứng
và \(\widehat{BAC}=\widehat{ECG}\) chứng minh tương tự ta có \(\Delta ACB=\Delta CGE\left(c.g.c\right)\)
suy ra \(\widehat{ACB}=\widehat{CGE}\)( 2 góc tương ứng )
mà 2 góc này ở vị trí đồng vị nên BC//EG (2)
từ (1) và (2) ta cí FE//BC;EG//BC mà theo tiên đề Ơ-clit thì qua điểm E nằm ngoài đường thẳng BC chỉ có 1 đường thẳng song song vói đường thẳng đó
nên FE trùng EG
hay F;E;G thẳng hàng
a) Xét tg MAB và tg MEC có :
M1 = M2 ( đối đỉnh)
BM = MC ( M là trung điểm BC)
MA = ME ( M là trung điểm AE)
=> Tg MAB = Tg MEC (cgc)
=> góc BAM = góc MEC
Mà 2 góc này ở vị trí so le trong => AB // CE
b) góc BAC = 180 - B1 - C1
góc C3 = 180 - C1 - C2
Mà C2 = B1 ( suy từ câu a)
=> góc BAC = góc C3 (*)
_ Xét tg ABC và tg CEG có:
góc BAC = C3 (cmt)
AB = CE
AC = CG ( C là trung điểm AG)
=> Tg ABC = tg CEG (cgc)
=> góc C1 = góc CGE
Mà 2 góc này ở vị trí đồng vị => BC // EG (1)
_ Xét tg BME và tg CMA có:
góc M3 = góc M4 ( đối đỉnh)
MB = MC (M là trung điểm BC)
ME = AM (M là trung điểm AE)
=> Tg BME = tg CMA (cgc)
=> EB = CA (-)
góc B2 = C1
_ góc B3 = 180 - B1 - B2
C3 = 180 - C2 - C1
Mà B1 = C2 ( suy từ câu a)
B2 = C1 (cmt)
=> góc B3 = C3
Mà góc C3 = góc BAC (*) => B3 = BAC
_ Xét tg FBE và tg BAC có :
góc B3 = BAC ( CMT)
BF = AB ( B là trung điểm AF)
BỂ = ÁC (-)
=> tg FBE = BAC (cgc)
=> góc BFE = ABC
Mà 2 góc này ở vị trí đồng vị
=> BC // FE (2)
_ Theo tiền đề ơ-clit, từ (1) và (2) => EG trùng với FE
=> BC // FG
Hay F, E, G thẳng hàng
-PMM-

Đã là tam giác ABC thì đương nhiên 3 điểm A; B; C không thẳng hàng
Xem lại đề bài