Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

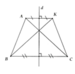
a) Đoạn thẳng đối xứng với AB, AC qua đường thẳng d lần lượt là KC, KB.
b) ta có AK//BC (vì cùng vuông góc với d) và AC = KB (tính chất đối xứng trục) Þ tứ giác AKCB là hình thang cân

a) Xét ΔABC vuông tại B và ΔAHB vuông tại H có
\(\widehat{BAH}\) chung
Do đó: ΔABC\(\sim\)ΔAHB(g-g)
b) Xét ΔCED vuông tại D và ΔBEH vuông tại H có
\(\widehat{CED}=\widehat{BEH}\)(hai góc đối đỉnh)
Do đó: ΔCED\(\sim\)ΔBEH(g-g)
Suy ra: \(\dfrac{CE}{BE}=\dfrac{CD}{BH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BH\cdot CE=CD\cdot BE\)(Đpcm)

a,Kẻ tam giác ABC sau đó nối C với K,B với K sẽ nhìn thấy đoạn thẳng đối xứng với AB và AC qua d.

A B C D d
a) Đxứng với AB qua d là KC, AC qua d là KB
b) Ta có: d là trung trực nên
AK\(\perp d;BC\perp d\)
hay AK//BC
=> AKCB là hình thang
lại có AC= KB ( AC đx với KB qua d)
=> hình thang AKCB là hình thang cân
a, Đoạn thẳng đối xứng với đoạn thẳng AB qua d là KC
Đoạn thẳng đối xứng với đoạn thẳng AC qua d là KB
b, Vì d là đường trung trực của AK và BC nên AK vuông góc với d và BC vuông góc với d. Vậy AK//BC, do đó AKCB là hình thang.
Theo câu a) AC đối xứng với KB qua d, do đó AC=KB. Hình thang AKCB có 2 đường chéo bằng nhau nên là hình thang cân