Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF

Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)
Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)

xét tam giác vuông BEC có EM là đường trung tuyến ứng với cạnh huyền
suy ra EM = \(\frac{1}{2}\)BC (1)
xét tam giác vuông CFB có FM là đường trung tuyến ứng với cạnh huyền
suy ra FM = \(\frac{1}{2}\)BC (2)
từ (1) và (2) suy ra M là trung điểm EF
mà M là trung điểm của BC
từ 2 điều đó suy ra BECF là hình bình hành
suy ra BE = CF

a, C/m ΔBME = ΔCMF
Xét ΔvBME và ΔvCMF. Ta có:
BM = CM (vì M là trung điểm của BC)
∠M1 = ∠M2 (đối đỉnh)
⇒ ΔvBME = ΔvCMF
b, C/m BE = CF
Ta có: ΔBME = ΔCMF (cmt)
⇒ BE = CF (hai cạnh tương ứng)
# chúc bẹn học tốt !!

Xét tam giác CFM và tam giác BEM có:
CFM = BEM = 900 (gt) vậy hai tam giác là 2 tam giác vuông
MB = MC (gt)
góc M1 = góc M2 (đổi đỉnh)
Vậy tam giác CFM = tam giác BEM (cạnh huyền - góc nhọn)
suy ra BE = CF ( hai cạnh tương ứng của 2 tam giác bằng nhau)
Nếu bạn chưa học trường hợp bằng nhau của tam giác thì có thể suy ra góc EBM = góc FCM vì phụ với góc M2 và góc M1 mà góc M1 = M2 vì đối đỉnh. suy ra 2 tam giác bằng nhau theo trường hợp góc - cạnh - góc nhé

`a,`
Ta có: \(\left\{{}\begin{matrix}\text{BE }\bot\text{ Ax}\\\text{CF }\bot\text{ Ax}\end{matrix}\right.\)
`@` Theo tiên đề Euclid
`-> \text {BE // CF}`
`b,`
Xét `2 \Delta` vuông `BEM` và `CFM`:
`\text {MB = MC (M là trung điểm của BC)}`
$\widehat {BME} = \widehat {CMF} (\text {2 góc đối đỉnh})$
`=> \Delta BEM = \Delta CFM (ch-gn)`
`c,`
Vì `\Delta BEM = \Delta CFM (b)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
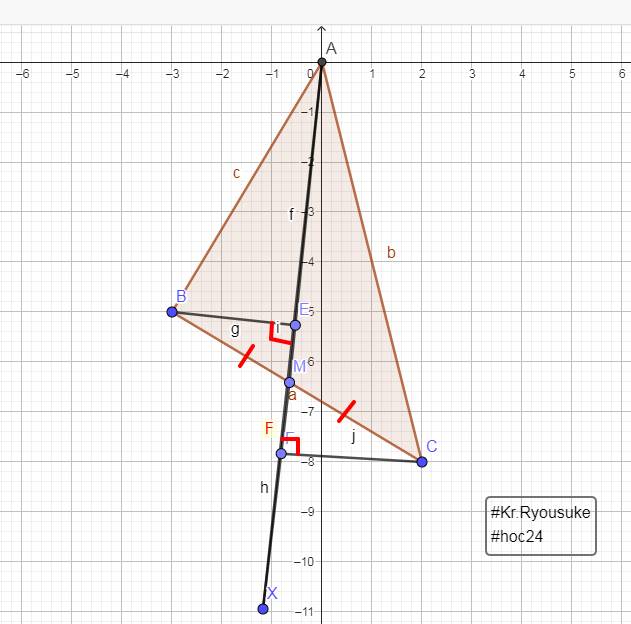
a:BE vuông góc AM
CF vuông góc AM
=>BE//CF
b: Xet ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc BME=góc CMF
=>ΔBEM=ΔCFM
b: ΔBEM=ΔCFM
=>BE=CF

Kí hiệu tam giác là t/g nhé
a) Có: BE _|_ Ax (gt)
CF _|_ Ax (gt)
Suy ra BE // CF (1)
Xét t/g EMB vuông tại E và t/g FMC vuông tại F có:
BM = CM (gt)
EMB = FMC ( đối đỉnh)
Do đó, t/g EMB = t/g FMC ( cạnh huyền và góc nhọn kề)
=> BE = CF (2 cạnh tương ứng) (2)
ME = MF (2 cạnh tương ứng) (3)
(1); (2) và (3) là đpcm
b) Xét t/g EMC và t/g FMB có:
EM = MF (câu a)
EMC = FMB ( đối đỉnh)
CM = BM (gt)
Do đó, t/g EMC = t/g FMB (c.g.c)
=> CE = BF (2 cạnh tương ứng) (4)
ECM = FBM (2 góc tương ứng)
Mà ECM và FBM là 2 góc so le trong
Nên EC // BF (5)
(4) và (5) là đpcm

câu sai nha bạn người ta bảo điều kiện của tam giác abc chứ ko phải thay canh BE với CE nha

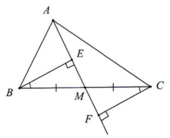
\(\Delta BEM=\Delta CFM\text{(cạnh huyền - góc nhọn) }\Rightarrow BE=CF\)