Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

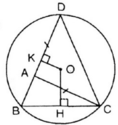
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
b) Vì BD > BC
⇒ 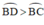
Kiến thức áp dụng
+ Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn
+ Trong một đường tròn, dây lớn hơn căng cung lớn hơn.

Cái này bạn chụp sách giải đúng ko ???
Sao cái này y chang như sách giải vậy ???

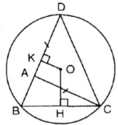
Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)

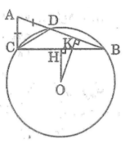
Theo câu a ,BC > BD
Vì trong một đường tròn, dây cung lớn hơn căng cung lớn hơn nên :
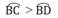

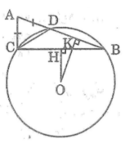
Áp dụng bất đẳng thức tam giác vào ΔABC , ta có: BC > AB - AC mà AC = AD (gt)
suy ra : BC > AB – AD hay : BC > BD
Vì trong một đường tròn ,dây cung lớn hơn gần tâm hơn nên: OH < OK

O B H C D K A
a) Xét tam giác ABC có :
BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
=> BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
=> OH > OK ( định lý về khoảng cách từ tâm đến dây )
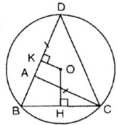
b) Vì BD > BC
\(\Rightarrow\widebat{BD}>\widebat{BC}\)

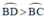
O K A B H C D
a) Trong ∆ABC, có BC < BA + AC.
Mà AC = AD suy ra BC < BD.
Theo định lí về dây cung và khoảng cách từ dây đến tâm, ta có OH > Ok.
b) Ta có BC < BD (cmt)
Nên suy ra BC < BD ( liên hệ cung và dây)