Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E M N
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
AB = AD (gt)
\(\widehat{DAE}=\widehat{BAC}\) (2 góc đối đỉnh)
AC = AE (gt)
\(\Rightarrow\Delta ABC=\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow\widehat{B}=\widehat{D}\) (2 góc tương ứng)
Xét \(\Delta ABM\) và \(\Delta ADN\) có:
\(\widehat{B}=\widehat{D}\) (cmt)
AB = AD (gt)
\(\widehat{BAM}=\widehat{DAN}\) (2 góc đối đỉnh)
\(\Rightarrow\Delta ABM=\Delta ADN\left(g.c.g\right)\)
\(\Rightarrow AM=AN\) (2 cạnh tương ứng) (đpcm)

Ta có hình vẽ sau:
A B C E D M N 1 2
a) Xét ΔABC và ΔADE có:
AB = AD (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) ( 2 góc đối đỉnh)
AC = AE (gt)
\(\Rightarrow\) ΔABC = ΔADE (c-g-c)
\(\Rightarrow\) \(\widehat{ADE}\) = \(\widehat{ABC}\) (2 góc tương ứng)
Mà hai góc này lại ở vị tí so le trong nên:
\(\Rightarrow\) BC // DE (đpcm)
b) Vì BC // DE (ý a) \(\Rightarrow\) \(\widehat{MEA}\) = \(\widehat{NCA}\) (cặp góc so le trong)
Xét ΔMAE và ΔNAC có:
\(\widehat{MEA}\) = \(\widehat{NCA}\) ( cm trên)
AE = AC (gt)
\(\widehat{MAE}\) = \(\widehat{NAC}\) ( 2 góc đối đỉnh)
\(\Rightarrow\) ΔMAE = ΔNAC (g-c-g)
\(\Rightarrow\) AM = AN ( 2 cạnh tương ứng) (đpcm)
Ta có hình vẽ:
A B C N M D E
a) Xét Δ DAE và Δ BAC có:
AD = AB (gt)
DAE = BAC (đối đỉnh)
AE = AC (gt)
Do đó, Δ DAE = Δ BAC (c.g.c)
=> DEA = BCA (2 góc tương ứng)
Mà DEA và BCA là 2 góc so le trong nên DE // BC (đpcm)
b) Vì DE // BC nên MDA = ABN (so le trong)
Xét Δ DAM và Δ BAN có:
MDA = ABN (cmt)
AD = AB (gt)
DAM = BAN (đối đỉnh)
Do đó, Δ DAM = Δ BAN (g.c.g)
=> AM = AN (2 cạnh tương ứng) (đpcm)

xét tam giác EAB và tam giác DAC có :
AB=AC ( tam giác ABC cân tại A )
góc EAB = góc DAC (đối đỉnh )
EA=AD (cmt)
-> tam giác EAB=tam giác DAC ( c.g.c)
-> góc EBA = góc DCA ( cặp góc tương ứng )
-> ED=DC ( cặp cạnh tương ứng )
*) tam giác ABC cân tại A -> góc B = góc C
mà góc EBA=góc DCA -> góc EBC= góc DCB
-> tan giác IBC cân tại I -> IB=IC
**) IB=IC ( cmt )
mà EB=DC
-> ID=IE
tam giác AED có AE=AD
-> tam giác AED cân tại A -> góc AED = góc EDA (1)
góc B = góc C (cmt) (2)
góc EAD = góc BAC ( đối đỉnh ) (3)
từ (1), (2), (3) -> góc AED = góc ACB
mà 2 góc ở vị trí so le trong -> ED//BC
ED cắt IA tại H
xét tam giác IEA và tam giác IDA (cm tương tự ) 2 tam giác = nhau theo trường hợp cạnh góc cạnh
-> I,H,A thẳng hàng (4)
vì ED//BC .
M là trung điểm của BC -> M cũng là trung điểm của ED
-> H , A , M thằng hàng (5)
từ (4) và (5) -> I ,A,M thẳng hàng

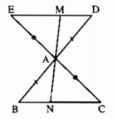
ΔAEM và ΔACN có:
∠C = ∠E ( hai góc so le trong, DE// BC)
AE = AC ( giả thiết)
∠EAM = ∠CAN (hai góc đối đỉnh)
⇒ ΔAEM = ΔACN (g.c.g) ⇒ AM = AN ( hai cạnh tương ứng).
