Question

[Phạm An Lành]

Cho tam giác ABC 

Có 1 đường thẳng đi qua A và // với BC và 1 đường thẳng đi qua C // với AB 

Hai đường thẳng đó cắt nhau tại D

Gọi M là giao điểm của cạnh BD và AC

a. Chứng minh M là trung điểm của AC

b. Đường thẳng D qua M cắt đoạn AD, BC lần lượt tại I và K

Chứng minh M là trung điểm của IK

Làm chi tiết và vẽ hình hộ với ạ

Answer 1

[Lê Song Phương]

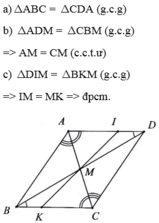
a) Vì AD//BC (gt) \(\Rightarrow\widehat{ADB}=\widehat{CBD}\)(hai góc so le trong)

Vì AB//CD (gt) \(\Rightarrow\widehat{ABD}=\widehat{CDB}\)(hai góc so le trong)

Xét \(\Delta ABD\)và \(\Delta CDB\), ta có: \(\widehat{ADB}=\widehat{CBD}\left(cmt\right);\widehat{ABD}=\widehat{CDB}\left(cmt\right)\); BD chung

\(\Rightarrow\Delta ABD=\Delta CDB\left(g.c.g\right)\)\(\Rightarrow AD=BC\)(hai cạnh tương ứng)

Mặt khác AD//BC \(\Rightarrow\widehat{MAD}=\widehat{MCB}\)(hai góc so le trong)

Xét \(\Delta MAD\)và \(\Delta MCB\)có \(\widehat{MAD}=\widehat{MCB}\left(cmt\right);AD=BC\left(cmt\right);\widehat{MDA}=\widehat{MBC}\left(cmt\right)\)

\(\Rightarrow\Delta MAD=\Delta MCB\left(g.c.g\right)\)\(\Rightarrow MA=MC\)(hai cạnh tương ứng)

Mà A,M,C thẳng hàng \(\Rightarrow\)M là trung điểm của AC (đpcm)

b) Xét \(\Delta AIM\)và \(\Delta CKM\)có \(\widehat{AMI}=\widehat{CMK}\)(hai góc đối đỉnh); \(AM=CM\left(cmt\right);\widehat{MAI}=\widehat{MCK}\left(cmt\right)\)

\(\Rightarrow\Delta AIM=\Delta CKM\left(g.c.g\right)\)\(\Rightarrow MI=MK\)(hai cạnh tương ứng) 

Mà I, M, K thẳng hàng \(\Rightarrow\)M là trung điểm của IK. (đpcm)

Answer 2

[Đặng Minh Đức]

ừeeargfegregrqe