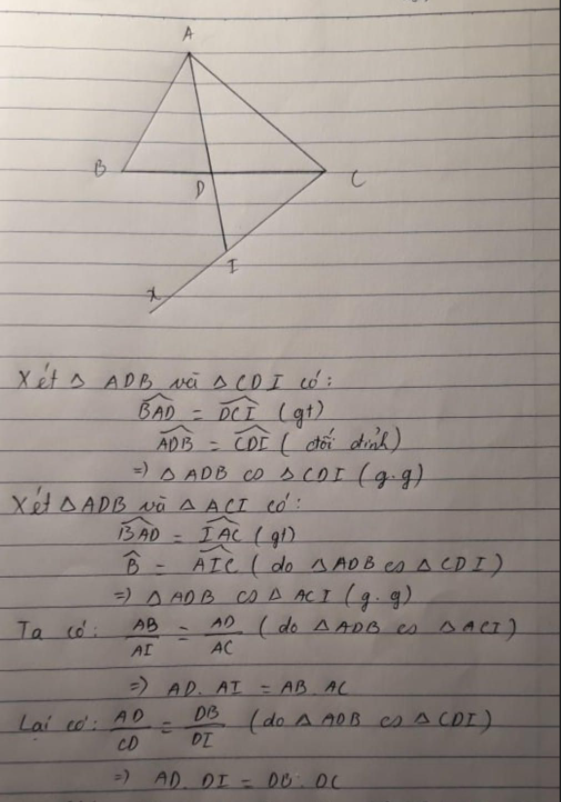Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải
A B C D I
a,
\(\widehat{DAC}=\widehat{BAD}=\widehat{DBI}\)( AD là tia phân giác \(\widehat{BAC}\) )
\(\widehat{ADC}=\widehat{BDI}\)
\(\Rightarrow\Delta ADC\sim\Delta BDI\left(g.g\right)\)
b, \(\Delta ADC\sim\Delta BDI\left(cmt\right)\Rightarrow\widehat{AIB}=\widehat{ACD}\)
\(\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABI\sim\Delta ADC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AI}=\dfrac{AD}{AC}\Rightarrow AB.AC=AD.AI\)

a: Xét ΔDAB và ΔDCI có
góc DAB=góc DCI
góc ADB=góc CDI
=>ΔDAB đồng dạng với ΔDCI
=>DA/DC=DB/DI
=>DA/DB=DC/DI
Xét ΔDAC và ΔDBI có
DA/DB=DC/DI
góc ADC=góc BDI
=>ΔDAC đồng dạng với ΔDBI
b: Xét ΔABD và ΔAIC có
góc ABD=góc AIC
góc bAD=góc IAC
=>ΔABD đồng dạng với ΔAIC
=>AB/AI=AD/AC
=>AB*AC=AD*AI

a) Xét \(\Delta ADB\) và \(\Delta CDE\) có ;
\(\widehat{ADB}=\widehat{CDE};\widehat{DAB}=\widehat{DCE}\)
\(\Rightarrow\) \(\Delta ADB\) ~ \(\Delta CDE\)
\(\Rightarrow\) \(\frac{AD}{CD}=\frac{BD}{DE}\) ; \(\frac{AD}{CD}=\frac{BD}{DE}\) ; \(\widehat{ABD}=\widehat{CED}\)
b) Xét \(\Delta BDE\) và \(\Delta ADC\) có :
\(\frac{AD}{CD}=\frac{BD}{DE}\) ; \(\widehat{BDE}=\widehat{ADC}\)
\(\Rightarrow\) \(\Delta BDE\) ~ \(\Delta ADC\)
\(\Rightarrow\) \(\widehat{DBE}=\widehat{DAC}\)
mà \(\widehat{DAC}=\widehat{BAD}=\widehat{BCE}\)
=> \(\widehat{DBE}=\widehat{BCE}\Rightarrow\Delta BCE\) cân tại E
c) Xét \(\Delta ADB\) và \(\Delta ACE\) có :
\(\widehat{ABD}=\widehat{CED}\) ; \(\widehat{BAD}=\widehat{EAC}\)
\(\Rightarrow\) \(\Delta ADB\) ~ \(\Delta ACE\)
\(\Rightarrow\) \(\frac{AD}{AC}=\frac{AB}{AE}\) \(\Rightarrow\) \(AD.AE=AC.AB\) (1)
Có : \(\frac{AD}{CD}=\frac{BD}{DE}\Rightarrow\) \(AD.DE=DB.CD\) (2)
Lấy (1) trừ (2) ta được :
\(AD.AE-AD.DE=AC.AB-BD.CD\)
\(\Rightarrow\) \(AD\left(AE-DE\right)=AC.AB-BD.CD\)
\(\Rightarrow AD^2=AC.AB-BD.CD\)
\(\Rightarrow AD^2+BD.CD=AC.AB\) (đpcm)

b) Xét ΔADB và ΔCDE có
\(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)
\(\widehat{BAD}=\widehat{ECD}\)(gt)
Do đó: ΔADB\(\sim\)ΔCDE(g-g)