Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE và ΔADC có
góc BAE=góc DAC
góc AEB=góc ACD
=>ΔABE đồng dạng với ΔADC
b: ΔABE đồng dạng với ΔADC
=>AE/AC=AB/AD
=>AE*AD=AB*AC=BE^2

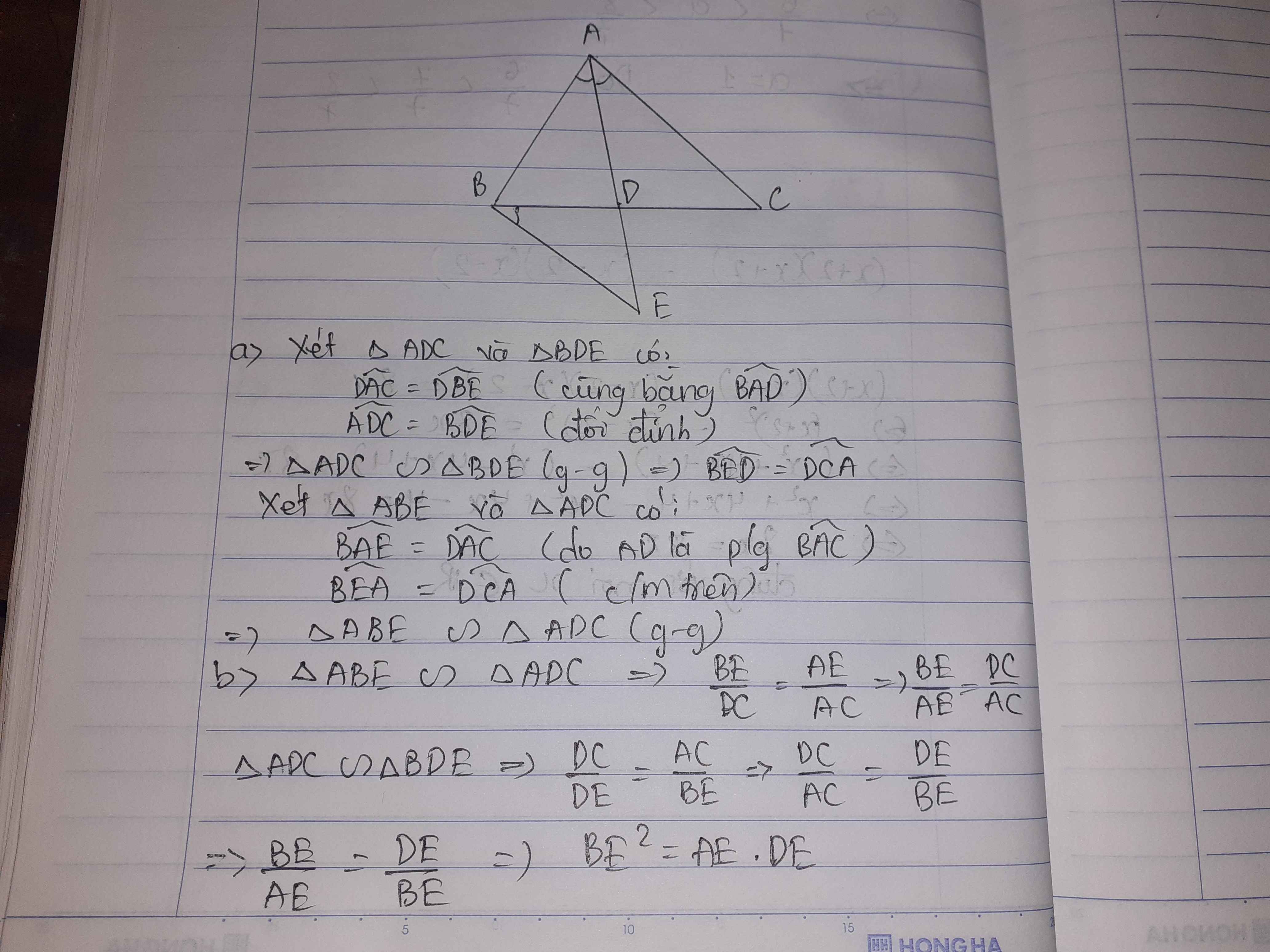
a) Xét ΔABE và ΔADC có
\(\widehat{BAE}=\widehat{DAC}\)(hai góc đối đỉnh)
\(\widehat{AEB}=\widehat{ACD}\)(ΔDBE\(\sim\)ΔDAC)
Do đó: ΔABE\(\sim\)ΔADC(g-g)

HÌNH TỰ KẺ NHA
1a) trong tam giác ADB có ADC là góc ngoài tại đỉnh D
=>góc ADC = góc BAD + góc ABD
mà góc BAD = góc DBE
=>góc ADC = góc ABD + góc DBE
=>góc ADB = góc ABE
Xét tam giác ADC va tam giác ABE
Góc BAD = góc CAD(AD là p/g tại đỉnh A)
góc ABE = góc ADC(cmt)
=> tam giác ABE đồng dạng với tam giác ADC(g.g)
1b) Xét tam giac AEB và tam giác BED
góc E chung
góc DBE = góc DAB(gt)
=>tam giác ABE đồng dạng vói tam giác BDE(g.g)
=>BE/DE = AE/BE
=>BE.BE=DE.AE
hayBE^2=DE.AE

a) Vì AD là tia phân giác ∠BAC => ∠BAD = ∠CAD
Mà ∠BAD = ∠CBE
Nên ∠CAD = ∠CBE
Xét ΔADC và ΔDEB có:
∠CAD = ∠CBE ( chứng minh trên )
∠ADC = ∠BDE ( đối đỉnh)
Do đó ΔADC đồng dạng với ΔDEB ( g.g)
b) Vì ΔADC đồng dạng với ΔDEB ( câu a)
=> ∠ACD = ∠BED ( 2 góc tương ứng )
Xét ΔADC có: ∠DAC + ∠DCA + ∠ADC = 180 độ
Xét ΔABE có: ∠BAE + ∠BEA + ∠ABE = 180 độ
Mà ∠DCA = ∠BEA ( chứng minh trên )
∠BAE = ∠CAD ( chứng minh trên )
=> ∠ADC = ∠ABE
c) Xét ΔABE và ΔBDE có:
∠BAE = ∠DBE ( giả thuyết)
∠E chung
Do đó ΔABE đồng dạng với ΔBDE (g.g)
=> EAEBEAEB = ABBDABBD
<=> EA . BD = EB . AB
<=>(EA . BD)² = (EB.AB)²