Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

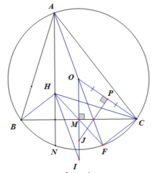
a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM

A B C D I R H K J M N O
Gọi M, N lần lượt là chân đường cao hạ từ B,C xuống AC,AB
Ta có \(DH.DA=DB.DC\)(1)
Để chứng minh K là trực tâm tam giác IBC ta chứng minh \(DK.DJ=DB.DC\)hay \(DK.DJ=DH.DA\)
Ta có NC,NA lần lượt là phân giác trong và phân giác ngoài của \(\widehat{MND}\)nên
\(\frac{HK}{HD}=\frac{NK}{ND}=\frac{AK}{AH}\)
\(\Rightarrow AK.HD=AD.HK\)
\(\Leftrightarrow HD\left(AD-DK\right)=AD\left(DK-DH\right)\)
\(\Leftrightarrow2.AD.DH=DK\left(DA+DH\right)\)
\(\Leftrightarrow2.AD.DH=2.DK.DJ\)
\(\Rightarrow AD.DH=DK.DJ\left(2\right)\)
Từ (1) và (2) ta có\(DK.DJ=DH.DA\)
=> K là trực tâm của tam giác IBC

a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a) Ta có \(\widehat{BNC}=\widehat{BMC}=90độ\)(gt)
Nên tứ giác BNMC nội tiếp (2 đỉnh N,M cùng BC với 2 góc bằng nhau)
(Câu sau không rõ. Cái gì là tâm đường tròn nội tiếp ΔMNH?)
b) Xét ΔAMN và ΔABC có:
\(\widehat{BAC}\)chung
\(\widehat{AMN}=\widehat{ABC}\)(tứ giác BNMC nội tiếp)
Do đó ΔAMN ~ ΔABC
Nên\(\frac{AM}{AB}=\frac{AN}{AC}\)
hay AM.AC=AN.AB
Ta có \(\widehat{ANH}=\widehat{AMH}=90độ\left(gt\right)\)
Nên \(\widehat{ANH}+\widehat{AMH}=180độ\)
Suy ra tứ giác ANHM nội tiếp
Do đó \(\widehat{NAM}+\widehat{NHM}=180độ\)
Mà \(\widehat{NHM}=\widehat{BHC}\)(đối đỉnh)
\(\widehat{BHC}=\widehat{BLC}\)(tính chất đối xứng trục)
Nên \(\widehat{NAM}+\widehat{BLC}=180độ\)
Suy ra tứ giác ABLC nội tiếp đường tròn (O) (tổng 2 góc đối bằng 180độ)
c) (Câu này hình như bạn ghi sai đề rồi, nếu I là giao điểm AH với AN thì I sẽ trùng với A. Nên mình nghĩ I là giao điểm MN với AH)
Ta có \(\widehat{HDC}=\widehat{HMC}=90độ\left(gt\right)\)
Nên \(\widehat{HDC+}\widehat{HMC}=180độ\)
Do đó tứ giác HMCD nội tiếp
Suy ra \(\widehat{HMD}=\widehat{HCD}\)
Mà \(\widehat{HCD}=\widehat{HMN}\)(tứ giác BMNC nội tiếp)
Nên \(\widehat{HMD}=\widehat{HMN}\)
Vậy MH là phân giác \(\widehat{NMD}\)
Mà MH vuông góc AM (gt)
Nên AM là phân giác ngoài
Do đó \(\frac{IH}{ID}=\frac{AH}{AD}\)
hay IH.AD=AH.ID
a.Ta có :
ˆAFH=ˆADB=90o→ΔAFH∼ΔADB(g.g)
→AFAD=AHAB→AF.AB=AH.AD
Tương tự AH.AD=AE.AC→AF.AB=AE.AC
b.Ta có :
ˆHFA=ˆHEA=ˆHFB=ˆHDB=90o
→AEHF,AEDB,FHDB nội tiếp
→ˆHFE=ˆFAE=ˆHBD=ˆHFD
→FH là phân giác ˆDFE
Mà FA⊥FH→FA là phân giác góc ngoài tại đỉnh F của ΔDEF
→HIHD=FIFD=AIAD
→IH.AD=AI.DH

Cho △ABC nhọn (AB<AC) nội tiếp (O), 2 đường cao BD và CE cắt nhau tại H
a/ Chứng minh : B,C,D,E cùng nằm trên một đường tròn .Xác định tâm M của đường tròn này.
b/ Chứng minh : OM // AH
c/ Chứng minh : AB.AE = AC.AD
d/ Gọi K là điểm đối xứng của H qua M .