Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

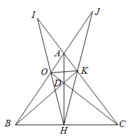
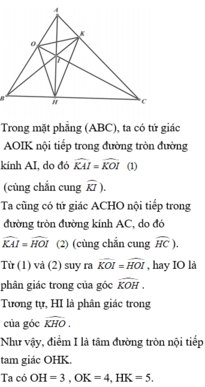
Ta có tứ giác BOKC là tứ giác nội tiếp đường tròn suy ra O K B ^ = O C B ^ 1
Ta có tứ giác KDHC là tứ giác nội tiếp đường tròn suy ra D K H ^ = O C B ^ 2
![]()
Do đó BK là đường phân giác trong của góc O K H ^ và AC là đường phân giác ngoài của góc O K H ^ .
Tương tự ta chứng minh được OC là đường phân giác trong của góc K O H ^ và AB là đường phân giác ngoài của góc K O H ^

Chọn D

Đáp án C
Vì OA, OB, OC đôi một vuông góc và H là trực tâm Δ A B C ⇒ O H ⊥ m p A B C
Khi đó d O ; A B C = O H = 3 ⇒ Phương trình mặt cầu là x 2 + y 2 + z 2 = 9

A B C d2 d1 H
A = AB giao d1=> Tọa độ A là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x+1=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x=-1\\y=\frac{1+4x}{3}\end{cases}\)<=> \(\begin{cases}x=-1\\y=-1\end{cases}\)=> A (-1; -1)
Đường thẳng d2 có vtpt là \(\vec{n_2}\left(7;2\right)\) chính là vtcp của đường thẳng AC , điểm A thuộc AC
=> Phương trình đường thẳng AC có dạng: \(\begin{cases}x=-1+7t\\y=-1+2t\end{cases}\)(t \(\in\) R)
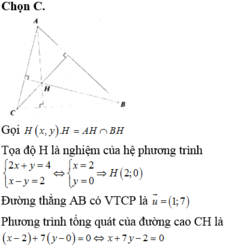
Gọi H = d1 \(\cap\) d2 => tọa độ H là nghiệm của pt: \(\begin{cases}7x+2y-22=0\\4x-3y+1=0\end{cases}\) <=> \(\begin{cases}x=\frac{64}{29}\\y=\frac{95}{29}\end{cases}\)=> H (\(\frac{64}{29};\frac{95}{29}\))
Đường cao CH đi qua H và có vtcp chính là vtpt của AB là \(\vec{n}\) (5; -3)
=> Phương trình CH có dạng : \(\begin{cases}x=\frac{64}{29}+5t\\y=\frac{95}{29}-3t\end{cases}\)
B = AB \(\cap\) d2 => Tọa độ B là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\7x+2y-22=0\end{cases}\) <=> \(\begin{cases}x=2\\y=4\end{cases}\)=> B (2;4)
Đường thẳng BC đi qua B , có vtcp chính là vtpt của d1 là \(\vec{n_1}\)(4;-3)
=> phương trình đường thẳng BC là: \(\begin{cases}x=2+4t\\y=4-3t\end{cases}\)