Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A K I D E H B F C
a ) Ta có : \(BD\perp AC,CE\perp AB\)
\(\Rightarrow\widehat{ADH}=\widehat{AEH}=90^0,\widehat{BDC}=\widehat{BEC}=90^0\)
\(\Rightarrow ADHE,BEDC\) nội tiếp
b . Ta có : \(\widehat{DHC}=\widehat{EHB},\widehat{HDC}=\widehat{HEB}=90^0\)
\(\Rightarrow\Delta HDC~\Delta HEB\left(g.g\right)\)
\(\Rightarrow\frac{HD}{HE}=\frac{HC}{HB}\Rightarrow HD.HB=HE.HC\)
c . Vì H là trực tâm \(\Delta ABC\Rightarrow AH\perp BC=F\)
Lại có : \(\widehat{AHD}=\widehat{CBF}\left(+\widehat{FAC}=90^0\right)\)
\(\widehat{AID}=\widehat{ACB}\Rightarrow\widehat{AID}=\widehat{AHD}\)
\(\Rightarrow\Delta AHI\) cân tại A
Mà \(AD\perp HI\Rightarrow AD\) là trung trực của HI \(\Rightarrow\)AC là đường trung trực của của HI.
d ) Từ câu c \(\Rightarrow AI=AH\)
Tương tự \(\Rightarrow AK=AH\Rightarrow A\) là tâm đường tròn ngoại tiếp \(\Delta HIK\)

a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Em không vẽ được hình, xin thông cảm
a, Ta có góc EAN= cungEN=cung EC+ cung EN
Mà cung EC= cung EB(E là điểm chính giữa cung BC)
=> góc EAN=cungEB+ cung EN=góc DFE (tính chất góc ở giữa)
=> tam giác AEN đồng dạng tam giác FED
Vậy tam giác AEN đồng dạng tam giác FED
b,Ta có EC=EB=EM
Tam giác EMC cân tại E => EMC=ECM
MÀ EMC+AME=180, ECM+ABE=180
=> AME = ABE
=> tam giác ABE= tam giác AME
=> AB=AM => tam giác ABM cân tại A
Mà AE là phân giác => AE vuông góc BM
CMTT => AC vuông góc EN
MÀ AC giao BM tại M
=> M là trực tâm tam giác AEN
Vậy M là trực tâm tam giác AEN
c, Gọi H là giao điểm OE với đường tròn (O) (H khác E) => O là trung điểm của EH
Vì M là trực tâm của tam giác AEN
=> \(EN\perp AN\)
Mà \(OI\perp AN\)(vì I là trung điểm của AC)
=> \(EN//OI\)
MÀ O là trung điểm của EH
=> I là trung điểm của MH (đường trung bình trong tam giác )
=> tứ giác AMNH là hình bình hành
=> AH=MN
Mà MN=NC
=> AH=NC
=> cung AH= cung NC
=> cung AH + cung KC= cung KN
Mà cung AH+ cung KC = góc KMC(tính chất góc ở giữa 2 cung )
NBK là góc nội tiếp chắn cung KN
=> gócKMC=gócKBN
Hay gócKMC=gócKBM
=> CM là tiếp tuyến của đường tròn ngoại tiếp tam giác MBK( ĐPCM)
Vậy CM là tiếp tuyến của đường tròn ngoại tiếp tam giác BMK

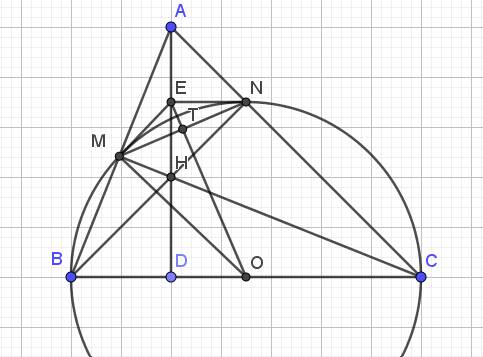
Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$