Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

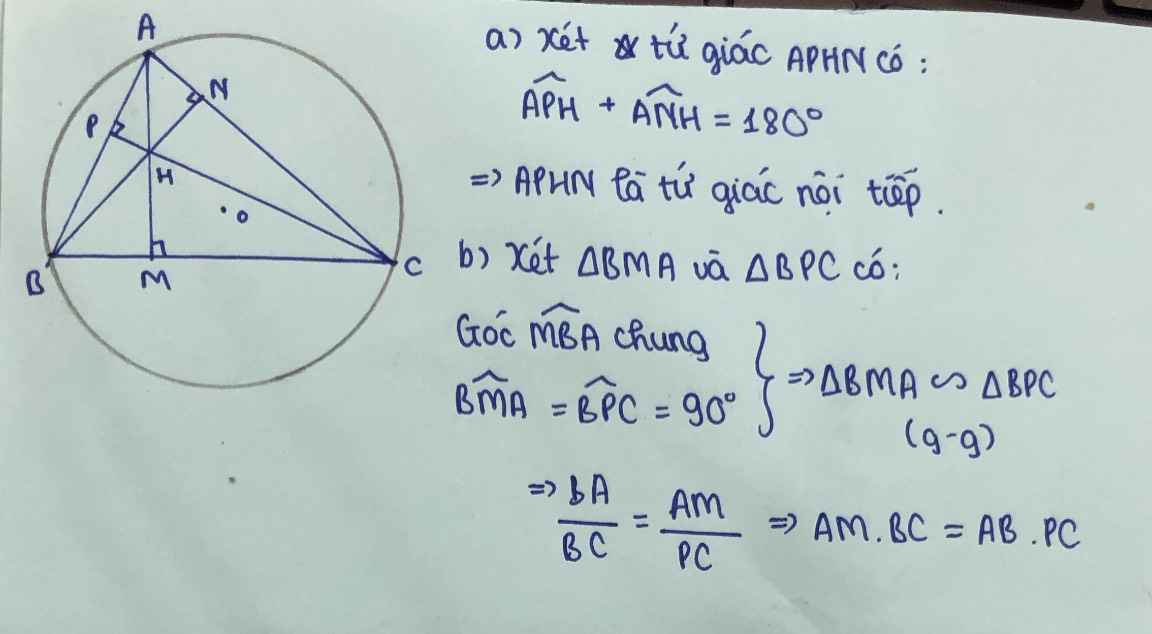
a) tứ giácAPHN có góc P+góc N =180 độnên nội tiếp đc
vìABDC là HBH nên HC song song BD,lại có CH vuông góc ABnên :góc ABD =90độ
chứng minh tương tự ta cũng có góc ACD=90 Độ
=> góc ABD+ góc ACD=180độ => tứ giác ABCD nôi tiếp đường tròn đường AD
b)Xét 2 tam giác ABE và ACH có :
ABE=ACH ( cùng phụ với BAC ) (1)
BAE phụ với BDA;BDA=BCA (góc nt cùng chắn CUNG AB )
CAH phụ với BCA(2)
Từ (1) và (2) suy ra 2 tam giác ABE, ACH đồng dạng
=>\(\dfrac{AB}{AE}=\dfrac{AC}{AH}=>AB\cdot AH=AE\cdot AC\)
C)
Gọi I là trung điểm BC => I cố định (Do B và C cố định)
Gọi O là trung điểm AD => O cố định ( Do BAC không đổi, B và C cố định, O là tâm đường tròn ngoại tiếp tam giác ABC )
=>độ dài OI không đổi
ABDC là hình bình hành => I là trung điểm HD
=>OI=\(\dfrac{1}{2}\)AH ( OI là đường trung bình tam giác ADH)
=>độ dài AH không đổi
Vì AH là đường kính đường tròn ngoại tiếp tứ giác APHN, độ dài AH không đổi => độ dài bán kính đường tròn ngoại tiếp tứ giác APHN không đổi => đường tròn ngoại tiếp tứ giác APHN có diện tích không đổi

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

a, Xét tứ giác BEHF có: góc BFH + góc BEH = 900 + 900 = 1800
=> Tứ giác BEHF nội tiếp.
b, Xét tứ giác AFEC có :
góc AFC = góc AEC ( = 900) (Hai góc cùng nhìn 1 cạnh dưới 1 góc vuông)
=> Tứ giác AFEC nội tiếp

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI