Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

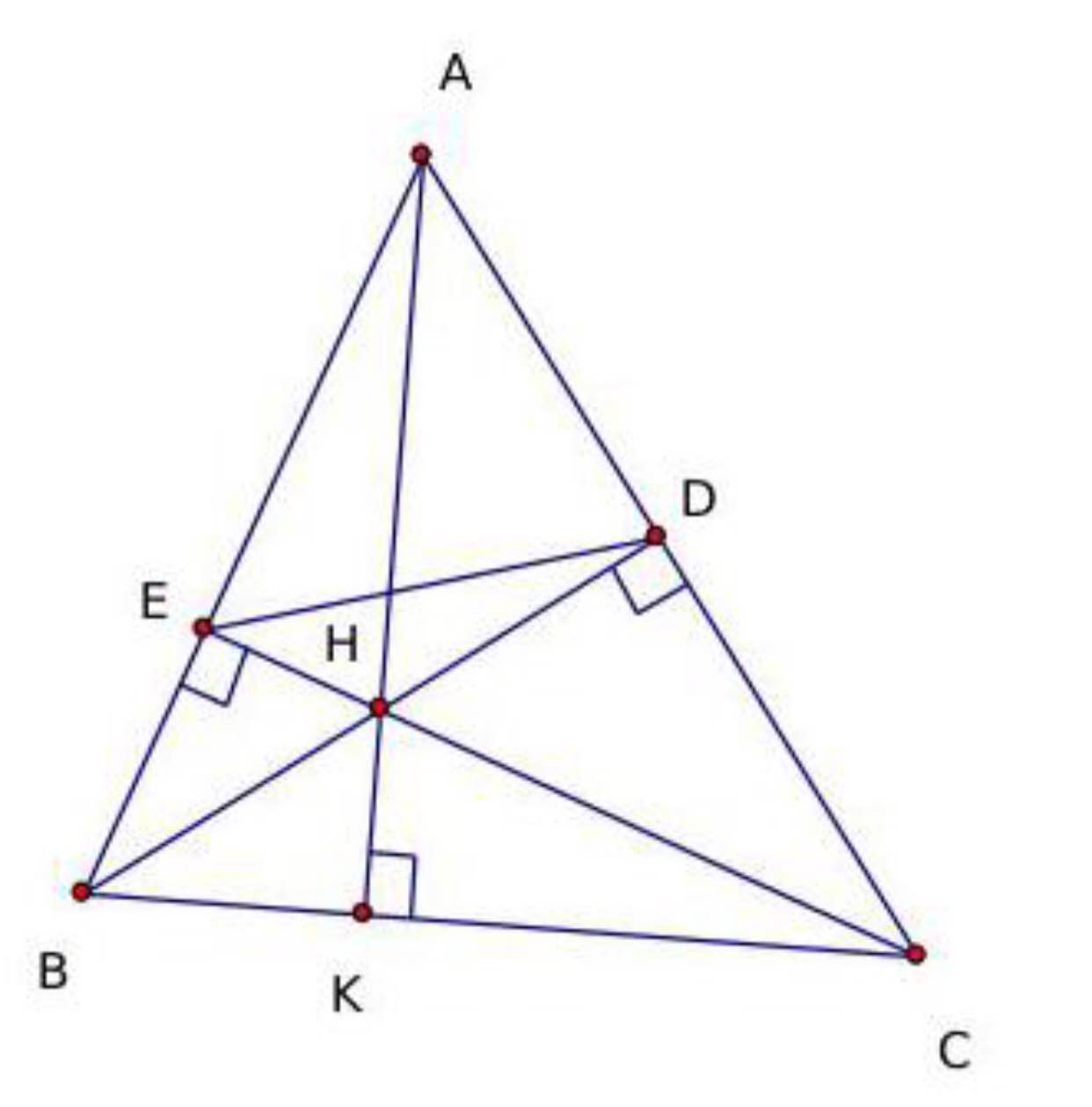
a: Xét ΔABC có
BD là đường cao ứng với cạnh AC
CE là đường cao ứng với cạnh AB
BD cắt CE tại H
Do đó: H là trực tâm của ΔBAC
hay AH\(\perp\)BC tại K
Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
\(\widehat{HBK}\) chung
Do đó: ΔBKH\(\sim\)ΔBDC
Suy ra: \(\dfrac{BK}{BD}=\dfrac{BH}{BC}\)
hay \(BH\cdot BD=BK\cdot BC\)

a) Ta có: \(\angle AEH+\angle ADH=90+90=180\Rightarrow AEHD\) nội tiếp (1)
Vì AK là đường kính \(\Rightarrow\angle ANK=90\)
\(\Rightarrow\angle ANH+\angle ADH=90+90=180\Rightarrow ANHD\) nội tiếp (2)
Từ (1) và (2) \(\Rightarrow A,N,E,H,D\) cùng thuộc 1 đường tròn
b) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp
\(\Rightarrow\angle ADE=\angle ABC\)
Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle ADE+\angle OAC=90\Rightarrow AO\bot DE\)
c) DE cắt BC tại Q'.Q'A cắt (O) tại N'
Xét \(\Delta Q'EB\) và \(\Delta Q'CD:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'EB=\angle Q'CD\\\angle CQ'Dchung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'EB\sim\Delta Q'CD\left(g-g\right)\Rightarrow\dfrac{Q'E}{Q'C}=\dfrac{Q'B}{Q'D}\Rightarrow Q'B.Q'C=Q'D.Q'E\)
Xét \(\Delta Q'N'B\) và \(\Delta Q'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'N'B=\angle Q'CA\\\angle CQ'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'N'B\sim\Delta Q'CA\left(g-g\right)\Rightarrow\dfrac{Q'N'}{Q'C}=\dfrac{Q'B}{Q'A}\Rightarrow Q'B.Q'C=Q'N'.Q'A\)
\(\Rightarrow Q'N'.Q'A=Q'D.Q'E\Rightarrow AN'DE\) nội tiếp
mà AEHD nội tiếp \(\Rightarrow A,N',D,E,H\) cùng thuộc 1 đường tròn
\(\Rightarrow N\equiv N'\Rightarrow Q\equiv Q'\Rightarrow\) đpcm

a, Áp dụng định lí Pitago
\(\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\\ =\dfrac{AK^2+KC^2+\left(BK+KC\right)^2-AB^2}{\left(BK+KC^2\right)+BA^2-\left(AK+KC\right)^2}\\ =\dfrac{2CK^2+2BK.CK}{2BK^2+2BK.Ck}\\ =\dfrac{2CK\left(CK+BK\right)}{2BK\left(BK+CK\right)}=\dfrac{CK}{BK}\)
b, Ta có
\(tanB=\dfrac{AK}{BK};tanC=\dfrac{AK}{CK}\\ Nên:tanBtanC=\dfrac{AK^2}{BK.CK}\left(1\right)\\ Mặt.khác.ta.có:\\ B=HKC\\ mà:tanHKc=\dfrac{KC}{KH}\\ Nên.tanB=\dfrac{KC}{KH}\\ Tương.tự.tanC=\dfrac{KB}{KH}\\ \Rightarrow tanB.tanC=\dfrac{KB.KC}{KH^2}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left(tanB.tanC\right)^2=\left(\dfrac{AK}{KH}\right)^2\\ Theo.GT:\\ HK=\dfrac{1}{3}AK\Rightarrow tanB.tanC=3\)
c, Chứng minh được
\(\Delta ABC.và.\Delta ADE.đồng.dạng\\ \Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\left(\dfrac{AB}{AD}\right)^2\left(3\right)\)
Mà
\(\widehat{BAC}=60^0\Rightarrow\widehat{ABD}=30^0\\\Rightarrow AB=2AD\left(4\right)\\ Từ.\left(3\right)và\left(4\right)=4\\ \Rightarrow S_{ADE}=30cm^2\)

\(VP=\frac{AH.AK+CH.CE+BH.BD+CH.CE-\left(AH.AK+BH.BD\right)}{BH.BD+CH.CE+AH.AK+BH.BD-\left(AH.AK+CH.CE\right)}\)
\(=\frac{2CH.CE}{2BH.BD}=\frac{CK.CB}{BK.BC}=\frac{KC}{KB}\) (DPCM)
lớn hơn thôi chứ nhỉ?