Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác EHD và tam giác FOC có: EHD=OFC=90; FED=FOC=(1/2 cung FD)=> đồng dạng=>EH.FC=HD.FO(1)
Xét tam giác DHF và OEB có :DHF=OEB=90; EFD=EOB=1/2 cung ED=>Đồng dạng=>HF.EB=HD.EO(2)
(1)va(2) suy ra: HF.EB=EH.FC(FO=EO)
mà góc HEB=góc HFC(AEF=AFE vì tam giác AEF cân tại A)
=>tam giác EHB đồng dạng tam giác FHC=>EHB=FHC
mình chứng minh vắn tắt thoy nha bn

Gọi G là giao điểm của AH và EF
Tứ giác AEHF là hình chữ nhật => AH = EF
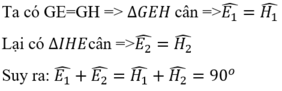
Do đó EF là tiếp tuyến của đường tròn (I)
Tương tự, EF là tiếp tuyến của đường tròn (K)

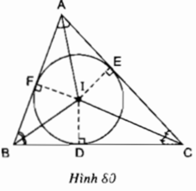
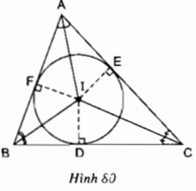
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

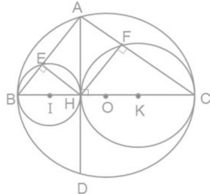
ΔAHB vuông nên AE.AB = AH2
ΔAHC vuông nên AF.AC = AH2
Suy ra AE.AB = AF.AC
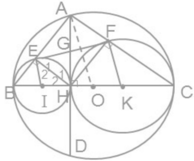

- Cách 1:
Ta có: EF = AH ≤ OA (OA có độ dài không đổi)
Do đó EF lớn nhất khi AH = OA
<=> H trùng O hay dây AD đi qua O.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
- Cách 2: EF = AH = AD/2.
Do đó EF lớn nhất khi AD lớn nhất. Khi đó, dây AD là đường kính.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

a/
\(\Delta\)vuông AHB có HE đường cao \(\Rightarrow\)AE.AB=AH2
\(\Delta\)vuông AHC có HF đường cao \(\Rightarrow\)AF.AC=AH2
\(\Rightarrow\)AE.AB=AF.AC
b/ CÁC PHƯƠNG PHÁP CHỨNG MINH TIẾP TUYẾN vd 2