Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)

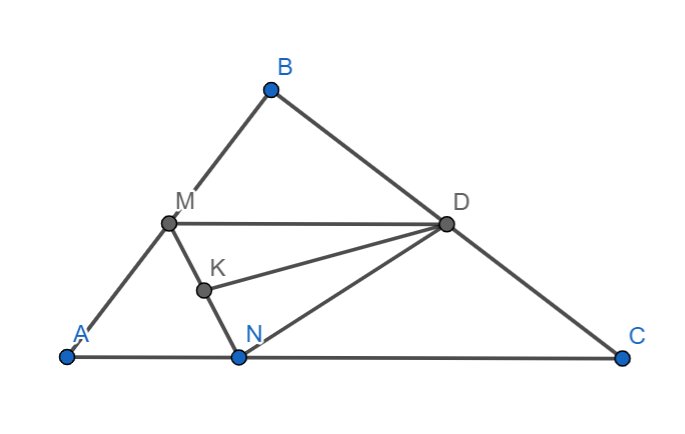
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong

A B C M N K
Theo các xác định điểm M, N ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.\)
Theo tính chất trung điểm của MN ta có:
\(\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\).

Câu 1:
Gọi E là trung điểm của KC
=>AK=KE=EC
Xét ΔBKC có CM/CB=CE/CK
nên ME//BK
Xét ΔAME có AI/AM=AK/AE
nên IK//ME
=>IK//BK
=>B,I,K thẳng hàng

A B C K I
a)
\(\overrightarrow{AK}=\overrightarrow{AI}+\overrightarrow{IK}=\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{IB}=\overrightarrow{AI}+\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{AB}\right)\)
\(=\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{IA}+\dfrac{1}{2}\overrightarrow{AB}\)\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AI}\).
b) Theo câu a:
\(\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}.\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\).