Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Vì AE//DF và DE//AF => AEDF là hình bình hành
Vậy AEDF là hình bình hành
b.ADEF là hình thoi <=> AD là phân giác góc BAC
ADEF là hình vuông <=> AEDF là hình thoi <=> AD là phân giác góc BAC
và A=90độ
Vậy...

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A

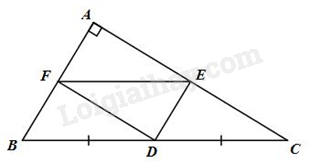
a) Ta có:
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat {{\rm{BAC}}} = 90^\circ \) và \(AB \bot AC\)
Mà \(DE\) // \(AB\) ; \(DF\) // \(AC\)
Suy ra \(DE \bot AC;\;DF \bot AB\)
Suy ra \(\widehat {DEA} = \widehat {DFA} = 90^\circ \)
Tứ giác \(AEDF\) có \(\widehat {BAC} = \widehat {DEA} = \widehat {DFA} = 90^\circ \) nên là hình chữ nhật
b) Vì \(AEDF\) là hình chữ nhật (cmt)
Suy ra \(AE = DF\); \(AF = DE\); \(AF\) // \(DE\); \(AE\) // \(DF\)
Vì \(DE \bot AC;\;DF \bot AB\) (cmt)
Suy ra \(\widehat {DEC} = \widehat {BFD} = 90^\circ \)
Xét \(\Delta BFD\) và \(\Delta DEC\) ta có:
\(\widehat {{\rm{BFD}}} = \widehat {{\rm{DEC}}} = 90^\circ \) (cmt)
\(BD = DC\) (gt)
\(\widehat {{\rm{FBD}}} = \widehat {{\rm{EDC}}}\) (do \(DE\) // \(BF\) )
Suy ra \(\Delta BFD = \Delta DEC\) (ch – gn)
Suy ra \(BF = DE\); \(DF = EC\) (hai cạnh tương tứng)
Xét tứ giác \(BFED\) ta có:
\(BF\) // \(DE\) (do \(AB\) // \(DE\))
\(BF = DE\) (cmt)
Suy ra \(BFED\) là hình bình hành

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
A E F C D B
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

DỄ THÔI phần a xét tứ giác AEDF có AF//DE(vì DE//AB gt)
AE//DF(vì DE//AB gt)
=> AEDF là hbh
phần b thì bt này thiếu dk tam giác ABC cân nữa mới lm đc