Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BDEF có
BD//EF
DE//BF
Do đó: BDEF là hình bình hành
Suy ra: BD=EF
b: Xét ΔADE và ΔEFC có
\(\widehat{ADE}=\widehat{EFC}\)
AD=EF
\(\widehat{A}=\widehat{FEC}\)
Do đó: ΔADE=ΔEFC
c: Ta có: BDEF là hình bình hành
nên Hai đường chéo BE và DF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của DF
nên M là trung điểm của BE
hay B,M,E thẳng hàng

Câu hỏi của Joen Jungkook - Toán lớp 7 - Học toán với OnlineMath

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD

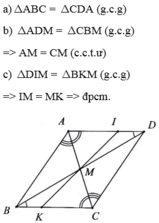
a: Xét ΔABC và ΔCDA có
\(\widehat{ACB}=\widehat{CAD}\)
AC chung
\(\widehat{CAB}=\widehat{ACD}\)
Do đó: ΔABC=ΔCDA
b: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
hay M là trung điểm của AC
c: Xét ΔAMI và ΔCMK có
\(\widehat{IAM}=\widehat{KCM}\)
AM=CM
\(\widehat{AMI}=\widehat{CMK}\)
Do đó: ΔAMI=ΔCMK
Suy ra: MI=MK
mà M,I,K thẳng hàng
nên M là trung điểm của IK



BD cắt AC tại O.
-△ABC=△CDA (g-c-g) \(\Rightarrow AB=DC\)
\(\Rightarrow\)△ABO=△CDO (g-c-g) \(\Rightarrow OA=OC\Rightarrow\)O là trung điểm AC.
-△ABC có: Trung tuyến BO cắt trung tuyến CE tại M.
\(\Rightarrow\)M là trọng tâm của △ABC mà F là trung điểm BC.
\(\Rightarrow\)A,M,F thẳng hàng.
cho mình xin hình