Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ABC đồng dạng với tam giác A'B'C' nên ta có:
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{1}{3}\)(vì \(\frac{AB}{A'B'}=\frac{2}{6}=\frac{1}{3}\)nên 1/3 là tỉ số đồng dạng
hay \(\frac{AC}{A'C'}=\frac{1}{3}\Leftrightarrow\)\(\frac{4}{A'C'}=\frac{1}{3}\Rightarrow A'C'=\frac{4.3}{1}=12\left(cm\right)\)
vậy .....................

a) Ta có: \(\frac{4}{8}=\frac{5}{10}=\frac{6}{12}\left(=\frac{1}{2}\right)\)
hay \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}\)
\(\Rightarrow\)\(\Delta A'B'C'~\Delta ABC\)
b) \(\Delta A'B'C'~\Delta ABC\)
\(\Rightarrow\)\(\frac{P_{A'B'C'}}{P_{ABC}}=\frac{A'B'}{AB}=\frac{8}{4}=2\)
Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !
Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber

+) Trong tam giác vuông A’B’C’ có \(\widehat{A'}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
A′B′2+A′C′2 =B′C′2
=> A′C′2=B′C′2−A′B′2=152−92=144
=> A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat{A}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
BC2=AB2+AC2= 62+82=100
Suy ra: BC = 10 (cm)
Ta có: \(\dfrac{A'B'}{AB}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(\dfrac{A'C'}{AC}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{B'C'}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
Suy ra: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}=\dfrac{3}{2}\)
Vậy ∆ A’B’C’ đồng dạng với ∆ ABC

Ta có
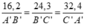
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm
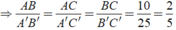
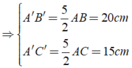
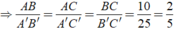
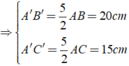

vì tam giác ABC đồng dạng với tam giác A'B'C' =>AB/A'B'=BC/B'C'=AC/A'C'
=>BC/B'C'=6/8=3/4=>BC=3.10/4=15/2(cm)
ta lại có AC/A'C'=3/4
=>A'C'/4=AC/3=3/1=3
=>AC=9cm=>A'C'=12(cm)
Vậy BC=15/2 cm ,AC=9cm,A'C'=12cm