Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
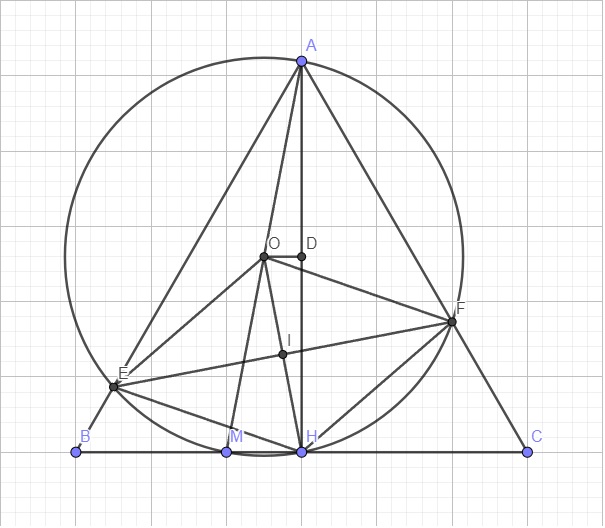
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H

1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)

Câu b: Xet tg vuông AEH và tg vuông ABC có
^BAH = ^ACB (cùng phụ với ^ABC)
=> Tg AEH đồng dạng với tg ABC \(\Rightarrow\frac{AE}{AC}=\frac{EH}{AB}\) mà EH=AF (cạnh đối HCN)
\(\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\Rightarrow AE.AB=AF.AC\)
Câu c:
Ta có AM=BC/2==BM=CM (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AMC cân tại M => ^MAC = ^ACB mà ^BAH = ^ACB (cmt) => ^MAC = ^BAH (1)
Ta có ^AHE = ^ABC (cùng phụ với ^BAH) mà ^AHE = ^HAC (góc so le trong) => ^ABC = ^HAC (2)
Gọi giao của AH với EF là O xét tg AOF có
AH=EF (hai đường chéo HCN = nhau)
O là trung điểm của AH vào EF
=> OA=OF => tg AOF cân tại O => ^HAC = ^AFE (3)
Từ (2) và (3) => ^AFE = ^ABC (4)
Mà ^ABC + ^ACB = 90 (5)
Từ (1) (4) (5) => ^MAC + ^AFE = 90
Xét tg AKF có ^AKF = 180 - (^MAC + ^AFE) = 180-90=90 => AM vuông góc EF tại K