Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D E F I G
a) Xét \(\Delta ABC\): \(D\)là trung điểm của \(BC\), \(E\)là trung điểm của \(AC\)\(\Rightarrow\)\(ED\)là đường trung bình của \(\Delta ABC\).
\(\Rightarrow ED\)//\(AB\)và \(ED=\frac{1}{2}AB\). \(F\)là trung điểm của \(AB\)\(\Rightarrow ED=AF=FB=\frac{1}{2}AB\)
\(ED\)//\(AB\Rightarrow ED\)//\(AF\Rightarrow ID\)//\(AF\). Mà \(FI\)//\(AD\).
\(\Rightarrow FI=AD\)và \(ID=AF\)(Tính chất đoạn chắn)
Mà \(ED=AF\Rightarrow ED=ID\).
Xét \(\Delta EDB\)và \(\Delta IDC:\)
\(DB=DC\)
\(\widehat{EDB}=\widehat{IDC}\)(Đối đỉnh) \(\Rightarrow\Delta EDB=\Delta IDC\)\(\left(c.g.c\right)\)
\(ED=ID\)
\(\Rightarrow\widehat{BED}=\widehat{CID}\)(2 góc tương ứng) và 2 góc này nằm ở vị trí so le trong \(\Rightarrow IC\)//\(BE\)
Đồng thời \(IC=BE\)(2 cạnh tương ứng)
b) \(AD\)//\(FI\Rightarrow\widehat{AGE}=\widehat{FHG}\Rightarrow\widehat{FHG}=90^0\)(Đồng vị). Mà \(BE\)//\(IC\)\(\Rightarrow\widehat{FHB}=\widehat{FIC}=90^0\)(Đồng vị)
\(\Rightarrow\Delta ICF\)là tam giác vuông tại \(I\).
Ta có: \(FI=AD\),\(IC=BE\)(cmt) \(\Rightarrow FI+IC+CF=AD+BE+CF\)(đpcm)


Tham khảo:
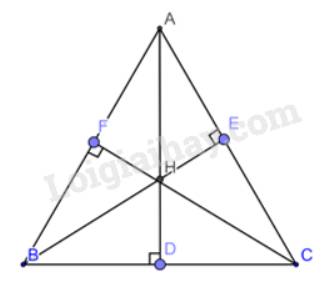
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
Ta có: ΔABC đều
mà AD,BE,CF là các đường trung tuyến
nên AD,BE,CF vừa là đường cao vừa là phân giác