Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Kẻ BK⊥ACBK⊥AC
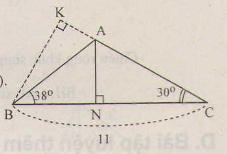
Ta được: ˆKBC=60∘KBC^=60∘ và ˆKBA=60∘=60∘−38∘=22∘KBA^=60∘=60∘−38∘=22∘
Xét tam giác KBC vuông tại K có:
BK=BC⋅sinC=11⋅sin30∘=5,5(cm)BK=BC⋅sinC=11⋅sin30∘=5,5(cm)
Xét tam giác KBA vuông tại K có:
AB=BKcos22∘=5,5cos22∘≈5,932(cm).AB=BKcos22∘=5,5cos22∘≈5,932(cm).
Xét tam giác ABN vuông tại N có:
AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)
b) Xét tam giác ANC vuông tại N có AC=ANsinC≈

Bài 2:
\(\cos60^0=\dfrac{28^2+35^2-BC^2}{2\cdot28\cdot35}\)
\(\Leftrightarrow2009-BC^2=980\)
hay \(BC=7\sqrt{21}\left(cm\right)\)

Kẻ đường cao BD (D thuộc AC)
Trong tam giác vuông ABD:
\(cosA=\dfrac{AD}{AB}\Rightarrow AD=AB.cosA=12.cos30^0=6\sqrt{3}\)
\(sinA=\dfrac{BD}{AB}\Rightarrow BD=AB.sinA=12.sin30^0=6\)
\(\Rightarrow CD=AC-AD=8\)
Áp dụng định lý Pitago cho tam giác vuông BCD:
\(BC=\sqrt{BD^2+CD^2}=10\left(cm\right)\)