Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

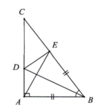
A B C E D
HÌNH KO CHUẨN LẮM
a) Xét \(\Delta ABD-\Delta EBD\) có :
BA = BE
\(\widehat{ABD}=\widehat{EBD}\)( phân giác )
DB là cạnh chung
=> \(\Delta ABD=\Delta EBD\)(C,G,C)
b) theo câu a) 2 tam giác ... = nhau
=> DA = DE ( 2 cạnh tương ứng )
c) theo câu a) 2 tam giác ... = nhau
=> \(\widehat{BAD}=\widehat{BED}=90^o\)( 2 góc tương ứng )
d) xét 2 tam giác \(\Delta EDB-\Delta EDC\)CÓ:
BED = CED ( góc vuông )
DE là cạnh chung
Để 2 tam giác \(\Delta EDB=\Delta EDC\) thì
\(\widehat{EBD}=\widehat{C}\)
MÀ \(\widehat{EBD}=\frac{1}{2}B\)
vậy để 2 tam giác đó = nhau thì góc B phải gấp 2 lần góc C

a/ Xét tam giác ABD và tam giác EBD có:
- Cạnh BD chung
- Góc ABD = góc DBE (vì BD là tia phân giác của góc ABE)
- BA = BE (gt)
Do đó tam giác ABD = tam giác EBD (c.g.c)
Suy ra DA = DE (2 cạnh tương ứng)
b/ Từ tam giác ABD = tam giác EBD => Góc A = góc BED (2 góc tương ứng)
Mà góc A = 90o nên góc EBD = 90o