
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



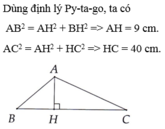
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)

Ta có:tam giác ABC có góc A=90 độ
=>Tam giác ABC vuông tại A.
Ta có:AB/AC=3/4 =>AB/3=AC/4
ÁP DỤNG T/C DÃY TỈ SỐ BĂNG NHAU.TA CÓ
AB/3=AC/4=AB2+AC2/32+42=152/9+16=225/25=9
=>AB=
=>AC=
Bạn hãy tính đi nhé

áp dụng đính lý PY_TA_GO ta có
BC^2 = AB^2 + AC^2
26^2 = AB^2 + AC ^2
=> 676 = AB^2 + AC^2
tuy vậy tỉ lệ giữa AB^2 và AC^2 vẫn là 5 : 12 vì cùng bình phương lên
ta có sơ đồ
AB^2 có 5 phần
AC^2 có 12 phần
tổng số phần là
5+ 12 = 17 (phần)
1 phần là
676 : 17 = 39 (cm)
đến đây cậu tính đc AB^2 và AC^2
từ đó tìm đc AB và AC
cái này liên quan đến định lý pitago nha bạn
do tg abc là tam giác vuông nên \(bc^2=ab^2+ac^2\)
=>\(ab^2+ac^2=26^2=676\)
Ta có tỉ lệ thức:\(\frac{ab}{5}=\frac{ac}{12}\)và ab^2+ac^2=676
\(ab=5k=>ab^2=\left(5K\right)^2=25.k^2\)
\(ac=12K=>ac^2=\left(12K\right)^2=144.K^2\)
ab+ac=\(25\cdot k^2+144\cdot k^2=k^2\cdot169\)
\(\frac{ab}{5}=\frac{ac}{12}\)=\(\sqrt{\frac{676}{169}}=2\)
=>\(ab=2\cdot5=10\\ ac=2\cdot12=24\)

a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: góc C=180-50-60=70 độ
Xét ΔABC có góc A<góc B<góc C
nên BC<AC<AB
Ta có: Tam giác ABC có góc A=90o
=>Tam giác ABC vuông tại A
=>AB2+AC2=BC2
Hay AB2+122=152
=>AB2+144=225
=>AB2=225-144
=>AB2=81
=>AB2=92
=>AB=9
Vậy AB=9cm