Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha.
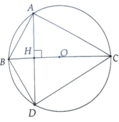
a, \(\Delta ABC\)có: \(OA=OB=OC=\frac{1}{2}BC\Rightarrow\Delta ABC\)vuông tại A
b, \(\left(O;R\right)\)có: \(AD\perp BC=\left\{H\right\}\Rightarrow\)H là trung điểm của AD (liên hệ giữa đường kính và dây)
\(\Delta ACD\)có: CH vừa là đường cao, vừa là đường trung tuyến \(\Rightarrow\Delta ACD\)cân tại C \(\Rightarrow AC=CD\)
Chứng minh tương tự ta có: \(\Delta ABD\)cân tại B có BC là đường cao \(\Rightarrow\)BC là phân giác của \(\widehat{ABD}\)
c, Chứng minh tương tự câu a ta có: \(\Delta BDC\)vuông tại D \(\Rightarrow\widehat{BDA}+\widehat{ADC}=90^o\)(2 góc nhọn phụ nhau) (1)
\(\Delta ABH\)có: \(\widehat{AHB}=90^o\Rightarrow\widehat{ABH}+\widehat{HAB}=90^o\)( 2 góc nhọn phụ nhau)
mà \(\widehat{DAB}=\widehat{BDA}\)(\(\Delta ABD\)cân tại B)
\(\Rightarrow\widehat{ABH}+\widehat{BDA}=90^o\)(2)
Từ (1), (2) \(\Rightarrow\widehat{ABH}=\widehat{ADC}\Leftrightarrow\widehat{ABC}=\widehat{ADC}\)

a, Vì AB//CD => góc AID=gocIDC
Ma IDC=ADI => AID=ADI => AI=AD
MaAI=IB=1/2AB => 2AD=AB