K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

30 tháng 12 2020
Ta có: HI/CH=1/2 HK / CH = EK / 2 EH = EK/DE
tam giác HIC đồng dạng tam giác EKD vì HI/CH=EK/DE và góc CHI = góc DEK ( cùng phụ góc HCK)
suy ra góc HCI = góc EDK
ta có: góc KDC + góc DCI = góc KDC + ( Góc HCI + góc HCD)
=(góc KDC + góc EDK) + góc HCD
= góc HDC + góc HCD
= 90 độ
suy ra DK vuông góc CI

VT
18 tháng 4 2020
Hình bạn tự vẽ nha!!
a.)Ta có:\(AH\perp BC\Rightarrow\widehat{AHB}=90^0\)
\(BE\perp AD\Rightarrow\widehat{AEB}=90^0\)
Xét tứ giác \(AEHB\)có:
\(\widehat{AHB}=\widehat{AEB}\left(=90^0\right)\)
Mà 2 góc này cùng nhìn \(AB\)
\(\Rightarrow\)Tứ giác\(AEHB\)nội tiếp (o)
\(\Rightarrow\)\(A,E,H,B\in\)đường tròn.
b.)Có tứ giác \(AEHB\)nội tiếp
\(\Rightarrow\widehat{DEH}=\widehat{HBA}\)
\(\Rightarrow\widehat{DEH}=\widehat{CBA}\)
Trong (o) có:\(\widehat{CDA}=\widehat{CBA}\)(2 góc nội tiếp chắn cung \(AC\))
\(\Rightarrow\widehat{CDA}=\widehat{DEN}\left(=\widehat{CBA}\right)\)
Mà 2 góc này ở vị trí SLT
\(\Rightarrow EH//CD\left(\text{đ}pcm\right)\)
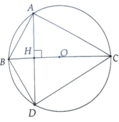
Hình bạn tự vẽ nha.
a, \(\Delta ABC\)có: \(OA=OB=OC=\frac{1}{2}BC\Rightarrow\Delta ABC\)vuông tại A
b, \(\left(O;R\right)\)có: \(AD\perp BC=\left\{H\right\}\Rightarrow\)H là trung điểm của AD (liên hệ giữa đường kính và dây)
\(\Delta ACD\)có: CH vừa là đường cao, vừa là đường trung tuyến \(\Rightarrow\Delta ACD\)cân tại C \(\Rightarrow AC=CD\)
Chứng minh tương tự ta có: \(\Delta ABD\)cân tại B có BC là đường cao \(\Rightarrow\)BC là phân giác của \(\widehat{ABD}\)
c, Chứng minh tương tự câu a ta có: \(\Delta BDC\)vuông tại D \(\Rightarrow\widehat{BDA}+\widehat{ADC}=90^o\)(2 góc nhọn phụ nhau) (1)
\(\Delta ABH\)có: \(\widehat{AHB}=90^o\Rightarrow\widehat{ABH}+\widehat{HAB}=90^o\)( 2 góc nhọn phụ nhau)
mà \(\widehat{DAB}=\widehat{BDA}\)(\(\Delta ABD\)cân tại B)
\(\Rightarrow\widehat{ABH}+\widehat{BDA}=90^o\)(2)
Từ (1), (2) \(\Rightarrow\widehat{ABH}=\widehat{ADC}\Leftrightarrow\widehat{ABC}=\widehat{ADC}\)