K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

LV
11 tháng 2 2020
Dựa vào tính chất đường trung bình của tam giác:
DM=EN/2
theo tính chất đương trung bình của hình thang:
EN=(DM+m)/2

CM
6 tháng 2 2018
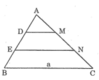
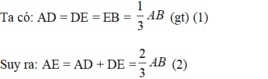
Trong ΔABC, ta có: DM // BC (gt)
Nên ![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra : ![]() (3)
(3)
Từ (1) và (3) suy ra: 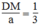
Suy ra: ![]()
Trong ΔABC, ta có: EN // BC (gt)
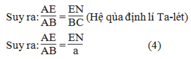
Từ (2) và (4) suy ra: 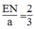 hay
hay 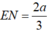

7 tháng 10 2021
Xét ΔAFH có
DE//FH
Do đó: \(\dfrac{DE}{FH}=\dfrac{AD}{AF}\)
\(\Leftrightarrow FH=2DE\)
Xét hình thang BDEC có
F là trung điểm của BD
FH//ED//BC
Do đó: H là trung điểm của EC
Xét hình thang BDEC có
F là trung điểm của BD
H là trung điểm của EC
Do đó: FH là đường trung bình của hình thang BDEC
Suy ra: \(FH=\dfrac{DE+BC}{2}\)
\(\Leftrightarrow DE=2\left(cm\right)\)
hay FH=4(cm)
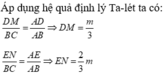
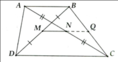
Ta có: \(AD=DE=EF=FB=\dfrac{1}{4}AB\) và \(AM=MN=NP=PC=\dfrac{1}{4}AC\)
Xét \(\Delta ABC\) có: \(\dfrac{AE}{AB}=\dfrac{AN}{AC}=\dfrac{1}{2}\)
\(\Rightarrow EN//BC\) \(\Rightarrow\) EN là đường trung bình của tam giác ABC
\(\Rightarrow EN=\dfrac{BC}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Tương tự với tam giác AEN có: \(\dfrac{AD}{AE}=\dfrac{AM}{AN}=\dfrac{1}{2}\)\(\Rightarrow DM//EN\)
\(\Rightarrow\)DM là đường trung bình của tam giác AEN
\(\Rightarrow DM=\dfrac{EN}{2}=\dfrac{7,5}{2}=3,75\left(cm\right)\)
Lại có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{2}{3}\)
Áp dụng định lí Ta-let đảo ta có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{EN}{FP}=\dfrac{2}{3}\Leftrightarrow\dfrac{7,5}{FP}=\dfrac{2}{3}\Rightarrow FP=11,25cm\)