Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai đường trung tuyến đã cho đều không phải là đường trung tuyến xuất phát từ A vì tọa độ của A không thỏa mãn các phương trình của chúng.
Đặt BM : 5x-3y-1=0 ; CN: y-3=0 là 2 trung tuyến của tam giác ABC.
Gọi M,N là trung tuyến xuất phát từ đỉnh B và C. Đặt B(x;y) => N((x-3)/2);((y-1)/2)) và B thuộc BM; C thuộc CN.<=> 5x-3y=0 và (y-1)/2-3=0 <=> x=21/5 và y=7 => B(21/5;7)
Tương tự => C(11/5;3)
=> BC(-2;-4) => n(4;-2). Vậy phương trình đường thẳng chứa cạnh BC là 4x-2y-54/5=0<=>10x-5y-27=0
Xét lại đáp án giúp mình với. Tại thấy hơi lẻ :)))

Cho tam giác abc có tọa độ A(-2;3) pt đường trung tuyến BM 2x-y+1=0 và CN x+y-4=0 M,N lần lượt là trung điểm AC và AB .TÌM tọa độ B

+) Phương trình đường cao qua B : 2x - y + 1 = 0
=> Phương trình AC có dạng : x + 2y + c = 0
Vì A ( 2; -1 ) thuộc AC => 2 + 2 ( -1 ) + c = 0 => c = 0
=> Phương trình AC: x + 2y = 0
=> Tọa độ điểm C thỏa mãn phương trình AC và đường cao qua C
nên là nghiệm của hệ pt: \(\hept{\begin{cases}x+2y=0\\3x+y+2=0\end{cases}}\)<=> C ( -4/5; 2/5)
+) Phương trình đường cao qua B : 3x + y + 2 = 0
=> Phương trình AB có dạng : x - 3y + b = 0
Vì A ( 2; -1 ) thuộc AB => 2 - 3 ( -1 ) + b= 0 => c = -5
=> Phương trình AB: x -3y -5 = 0
=> Tọa độ điểm B thỏa mãn phương trình AB và đường cao qua CB
nên là nghiệm của hệ pt: \(\hept{\begin{cases}2x-y+1=0\\x-3y-5=0\end{cases}}\)<=> C ( -8/5; -11/5)
+) M là trung điêm BC => M ( -6/5; -9/10 )
Mà A ( 2; -1)
=> \(\overrightarrow{MA}=\left(\frac{16}{5};-\frac{1}{10}\right)\)
=> MA có véc tơ pháp tuyến: ( 1/10; 16/5)
=> Viết phương trình MA : 1/10 ( x- 2 ) + 16/5 ( y+ 1 ) = 0
<=> x + 32y+ 30 = 0

Đáp án A
Gọi AI là đường cao kẻ từ đỉnh A của tam giác. Gọi M là trực tâm của tam giác ABC
Khi đó tọa độ điểm M thỏa mãn hệ phương trình
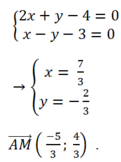
Đ ư ờ n g t h ẳ n g A I q u a M ( 7 3 ; - 2 3 ) v à n h ậ n n → ( 4 ; 5 ) l à m V T P T .
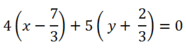
Hay 4x+ 5y – 6= 0

Thay tọa độ A vào 2 pt trung tuyến đều không thỏa mãn
\(\Rightarrow\) 2 trung đó đó xuất phát từ B và C, giả sử trung tuyến xuất phát từ B có pt x-2y+1=0 và từ C có pt y=1
\(\Rightarrow B\left(2b-1;b\right)\) ; \(C\left(c;1\right)\)
Gọi G là trọng tâm tam giác \(\Rightarrow\) G là giao điểm 2 trung tuyến nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-2y+1=0\\y=1\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}1+2b-1+c=3.1\\3+b+1=3.1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2b+c=3\\b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-1\\c=5\end{matrix}\right.\)
\(\Rightarrow B\left(-3;-1\right)\) ; \(C\left(5;1\right)\)
Biết 3 tọa độ 3 đỉnh của tam giác, dễ dàng viết được phương trình các cạnh

H là trực tâm của tam giác nhỉ.
A có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x-2y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\Rightarrow A\left(-1;0\right)\)
B có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow B\left(0;2\right)\)
H có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}x-2y+1=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow H\left(0;\dfrac{1}{2}\right)\)
Phương trình đường thẳng AC: \(y=0\)
Phương trình đường thẳng CH: \(x+2y-1=0\)
C có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}y=0\\x+2y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\Rightarrow H\left(1;0\right)\)

Do BC vuông góc đường cao AH kẻ từ A nên BC nhận (3;4) là 1 vtpt
Phương trình BC:
\(3\left(x+4\right)+4\left(y-0\right)=0\Leftrightarrow3x+4y+12=0\)
C là giao điểm BC và trung tuyến kẻ từ C nên tọa độ C là nghiệm:
\(\left\{{}\begin{matrix}4x+y+3=0\\3x+4y+12=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-3\end{matrix}\right.\) \(\Rightarrow C\left(0;-3\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\) thuộc trung tuyến kẻ từ C nên tọa độ M có dạng: \(M\left(m;-4m-3\right)\)
Áp dụng công thức trung điểm: \(\left\{{}\begin{matrix}x_A=2x_M-x_B=2m+4\\y_A=2y_M-y_B=-8m-6\end{matrix}\right.\)
Do A thuộc -4x+3y+2=0 nên:
\(-4\left(2m+4\right)+3\left(-8m-6\right)+2=0\Rightarrow m=-1\) \(\Rightarrow A\left(2;2\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-6;-2\right)\Rightarrow\) đường thẳng AB nhận (1;-3) là 1 vtpt
Phương trình AB:
\(1\left(x+4\right)-3\left(y-0\right)=0\Leftrightarrow x-3y+4=0\)
\(\overrightarrow{AC}=\left(-2;-5\right)\Rightarrow\) đường thẳng AC nhận (5;-2) là 1 vtpt
Phương trình AC:
\(5\left(x-2\right)-2\left(y-2\right)=0\Leftrightarrow5x-2y-6=0\)
b.
Ta có: \(\overrightarrow{AB}=\left(-6;-2\right)\Rightarrow AB=\sqrt{\left(-6\right)^2+\left(-2\right)^2}=2\sqrt{10}\)
Gọi H là chân đường cao hạ từ C xuống AB
\(\Rightarrow CH=d\left(C;AB\right)=\dfrac{\left|0-\left(-3\right).3+4\right|}{\sqrt{1^2+\left(-3\right)^2}}=\dfrac{13\sqrt{10}}{10}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}CH.AB=13\)
Do B thuộc BH nên tọa độ có dạng \(B\left(b;2b+3\right)\)
Gọi E là trung điểm AB \(\Rightarrow E\left(\dfrac{b+1}{2};b+3\right)\)
Do E thuộc CE nên:
\(\dfrac{b+1}{2}+b+3-2=0\Rightarrow b=-1\) \(\Rightarrow B\left(-1;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-2;-2\right)\Rightarrow\) đường thẳng AB nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x-1\right)-1\left(y-3\right)=0\Leftrightarrow x-y+2=0\)
E(x;-x+2)
Theo đề, ta có: \(\left\{{}\begin{matrix}x=\dfrac{1+x_B}{2}\\-x+2=\dfrac{3+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+1=2x\\y_B+3=-2x+4\end{matrix}\right.\)
=>B(2x-1;-2x+1)
vecto AB=(2x-2;-2x-2)
BH: 2x-y+3=0
=>VTPT là (2;-1)
=>VTCP là (1;2)
Theo đề, ta có: 1(2x-2)+2(-2x-2)=0
=>2x-2-4x-4=0
=>-2x-6=0
=>x=-3
=>B(5;-5)
vecto AB=(4;-8)
=>VTPT là (8;4)
Phương trình AB là:
8(x-5)+4(y+5)=0
=>2(x-5)+y+5=0
=>2x-10+y+5=0
=>2x+y-5=0