Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Do MP//AC nên Đường cao hạ từ P xuống AC = đường cao hạ từ P xuống AC
Xét tg AMC và tg APC có AC chung nên
S(AMC) / S(APC) = Đường cao hạ từ P xuống AC / đường cao hạ từ P xuống AC = 1
=> S(AMC) = S(APC)
b/ Xét tg APC và tg ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{2}{3}\Rightarrow S_{APC}=S_{AMC}=\frac{2xS_{ABC}}{3}=\frac{2x516}{3}=344cm^2\)

(Cái dữ liệu tìm diện tích tam giác BED là bỏ nha bạn)
A B C N P a M
\(S_{BMa}=S_{AMa}\Rightarrow S_{BMN}=S_{AaN}\)
\(S_{CMP}=S_{AMP}\Rightarrow S_{CMN}=S_{APN}\)
\(\Rightarrow S_{MBC}=S_{BMN}+S_{CMN}=S_{AaN}+S_{APN}=S_{APa}=\frac{1}{3}S_{ABC}\)
\(\Rightarrow S_{BCM}=516:3=172cm^2\)

S(BMQ) = S(AMQ) => S(BMN) = S(AQN)
S(CMP) = S(AMP) => S(CMN) = S(APN)
=> S(MBC) = S(BMN) + S(CMN) = S(AQN) + S(APN) = S(APQ) = 1/3 x S(ABC)
=> S(MBC) = 516 : 3 = 172 (cm2)
Đáp án:
172cm2
Giải thích các bước giải:
Hình mình ko biết vẽ chỗ nào trên máy tính nên mong bn thông cảm ạ !
S(BMQ)=S(AMQ)=>S(MNQ)=S(AMQ)
S(CMP)=S(AMP)=> S(CMP)=S(AMP)
=>S(MBC)=S(BMN)+S(CMN)=S(AQN)+S(APN)=S(APQ)=`1/3`x S(ABM)
=>S(MBC)=516 : 3 = 172 ( cm2 )
Đáp số : 172 cm2

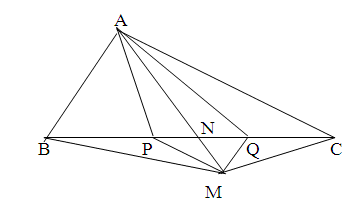
S(BMQ) = S(AMQ) => S(BMN) = S(AQN)
S(CMP) = S(AMP) => S(CMN) = S(APN)
=> S(MBC) = S(BMN) + S(CMN) = S(AQN) + S(APN) = S(APQ) = 1/3 x S(ABC)
=> S(MBC) = 516 : 3 = 172 (cm2)