Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+Ta có AB và CH vuông góc với nhau nên đường thẳng AB nhận u → ( 1 ; - 1 ) làm VTCP và n → ( 1 ; 1 ) làm VTPT.
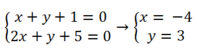
Đường thẳng AB nhận (1 ; 1) làm VTPT và đi qua điểm A( 1 ; -2) nên có phương trình là :
1( x-1) + 1( y+ 2) =0 hay x+ y+ 1= 0
+ Mà 2 đường thăng AB và BN cắt nhau tại B nên Toạ độ B là nghiệm hệ phương trình
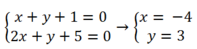
Vậy tọa độ điểm B( -4 ; 3) .

Đáp án D
Ta có AB và CH vuông góc với nhau nên AB qua A(1; -2) và nhận VTPT ( 1;1). Phương trình AB:
1(x-1) + 1( y+2) = 0 hay x+ y +1 = 0
Có AB và BN cắt nhau tại B nên tọa độ B là nghiệm hệ phương trình
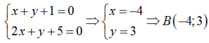

Tọa độ điểm B là nghiệm của hệ phương trình :
\(\left\{{}\begin{matrix}x-y+2=0\\2x-y+8=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-4\end{matrix}\right.\Rightarrow B\left(-6;-4\right)\)
Ta có : \(\overrightarrow{n_{BH}}=\overrightarrow{u_{AC}}=\left(1;-1\right)\Rightarrow\overrightarrow{n_{AC}}=\left(1;1\right)\)
Phương trình đường thẳng AC đi qua \(A\left(3;2\right)\) và nhận \(\overrightarrow{n_{AC}}=\left(1;1\right)\) làm VTPT :
Suy ra AC : \(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi \(M\left(a;b\right)\Rightarrow2a-b+8=0\Rightarrow b=2a+8\) ( Vì M thuộc BM )
Do đó \(M\left(a;2a+8\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=2x_M-x_A=2a-3\\y_C=2y_M-y_A=4a+14\end{matrix}\right.\)
Mà \(C\in AC\Rightarrow2a-3+4a+14-5=0\Leftrightarrow a=-1\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=-5\\y_C=10\end{matrix}\right.\) . Vậy \(C\left(-5;10\right)\)

AB vuông góc CH nên nhận \(\left(1;1\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
B là giao điểm BN và AB nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}2x+y+5=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow B\left(-8;11\right)\)
Gọi D là điểm đối xứng A qua BN \(\Rightarrow D\in BC\)
Phương trình đường thẳng d qua A và vuông góc BN (nên nhận \(\left(1;-2\right)\) là 1 vtpt) có dạng:
\(1\left(x-1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+3=0\)
Gọi E là giao điểm d và BN \(\Rightarrow E\) là trung điểm AD
Tọa độ E là nghiệm: \(\left\{{}\begin{matrix}2x+y+5=0\\x-2y+3=0\end{matrix}\right.\) \(\Rightarrow E\left(-\dfrac{13}{5};\dfrac{1}{5}\right)\)
\(\Rightarrow D\left(-\dfrac{31}{5};-\dfrac{8}{5}\right)\Rightarrow\overrightarrow{BD}=\left(\dfrac{9}{5};-\dfrac{63}{5}\right)=\dfrac{9}{5}\left(1;-7\right)\)
\(\Rightarrow\) Đường thẳng BC nhận (7;1) là 1 vtpt
Phương trình BC:
\(7\left(x+8\right)+1\left(y-11\right)=0\Leftrightarrow7x+y+45=0\)

Cô xóa giúp em câu kia với ạ! Tọa độ đỉnh\(B\left(\frac{32}{17};\frac{49}{17}\right)\)và C\(\left(-\frac{8}{17};\frac{6}{17}\right)\)
Gọi đường phân giác AD: x+y-3=0, đường trung tuyến BM: x-y+1=0 và đường cao CH: 2x+y+1=0
Mà A \(\in\)AD => \(A\left(a;3-a\right);B\in BM\Rightarrow B\left(b;b+1\right);C\in CH\Rightarrow C\left(c;-2c-1\right)\)
Có M là trung điểm AC nên M\(\left(\frac{a+c}{2};\frac{2-a-2c}{2}\right)\)
Mà M\(\in\)BM nên thay vào phương trình BM ta có: \(\frac{a+c}{2}-\frac{2-a-2c}{2}+1=0\Leftrightarrow2a+3c=0\left(1\right)\)
Ta có: \(\overrightarrow{AB}=\left(b-a;a+b-2\right)\)do \(AB\perp\)CH => \(\overrightarrow{AB}\cdot\overrightarrow{u_{CH}}=0\Leftrightarrow3a+b=4\left(2\right)\)
Trong đó \(\overrightarrow{u_{CH}}\)=(1;-2) là một vecto chỉ phương của đường cao CH
Gọi I là giao của BM và AD. Nhận thấy AD _|_BM tại I nên I là trung điểm của BM
Do đó \(I\left(\frac{a+2b+c}{4};\frac{-a+2b-2c+4}{4}\right)\)mà I\(\in\)AD => 4b-c=8(3)
Từ (1)(2)(3) ta có \(a=\frac{12}{17};b=\frac{32}{17};c=\frac{-8}{17}\)
Kết luận \(A\left(\frac{12}{17};\frac{39}{17}\right),B\left(\frac{32}{17};\frac{49}{17}\right),C\left(\frac{-8}{17};\frac{6}{17}\right)\)
Lần sau em đăng vào học 24 nhé!
Hướng dẫn:
Gọi BM là đường trung tuyến kẻ từ B; AD là phân giác kẻ từ A; CH là đường cao kẻ từ C
A ( a; 3 - a); C ( c: -2c -1 )
Có M là trung điểm AC => M ( a+c/2 ; 2-a-2c/2)
=> Gọi I là giao điểm của AD và BM => chứng minh I là trung điểm BM
=> tìm đc tọa độ B theo a và c
Mà B thuộc MB => thay vào có 1 phương trình theo ẩn a và c
Lại có: AB vuông CH => Thêm 1 phương trình theo a và c
=> Tìm đc a, c => 3 đỉnh

A. 2x + y + 3 = 0
B. 2x + 3y - 8 = 0
C. 2x + 3y + 8 = 0
D. 3x - 2y + 1 = 0
$BC$ có vectơ chỉ phương là: $\overrightarrow{BC}=(2;3)$
Gọi $H$ là chân đường cao hạ từ $A$ xuống $BC$
$\Rightarrow AH$ có vectơ pháp tuyến là: $\overrightarrow{BC}=(2;3)$
$AH:2x+3y-8=0$
Chọn đáp án: $B$