Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\left(c.cosC-b.cosB\right)=a.\left(c.\dfrac{a^2+b^2-c^2}{2ab}-b.\dfrac{a^2+c^2-b^2}{3ac}\right)\)
\(=\dfrac{\left(a^2+b^2-c^2\right)c^2}{2bc}-\dfrac{\left(a^2+c^2-b^2\right)b^2}{2bc}\)
\(=\dfrac{\left(b^2-c^2\right)\left(b^2+c^2-a^2\right)}{2bc}=\left(b^2-c^2\right)cosA\)

A B C I D F J
Bổ đề: Tam giác ABC cân tại A. Điểm D nằm trên trung trực của BC khi và chỉ khi \(\widehat{ADB}=\widehat{ADC}\).
Giải: Vì \(CD=CA\), điểm I nằm trên phân giác \(\widehat{ACD}\) nên \(ID=IA\)
Ta thấy (J) tiếp xúc với CA tại A, suy ra \(\widehat{AFI}=\widehat{IAC}=\widehat{IAF}\) hay \(IA=IF\)
Từ đó \(\Delta DIF\) cân tại I. Chú ý rằng \(\widehat{IBF}=\widehat{IBD}\), suy ra \(BF=BD\) theo bổ đề.

Cách làm
1. Từ phương trình 3 cạnh suy ra tọa độ 3 đỉnh của tam giác
2. Gọi D là chân đường phân giác trong góc A của ΔABC ⇒ \(\overrightarrow{BD}=\dfrac{AB}{AC}.\overrightarrow{DC}\)
3. Tâm đường tròn ngoại tiếp I của tam giác ABC là chân đường phân giác trong góc B của ΔABD

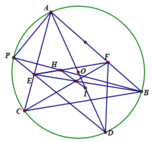
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.
Gọi tia AI cắt cạnh BC tại M. Đặt \(S_{AMB}=S_C;S_{BMC}=S_A;S_{CMA}=S_B\)
\(\overrightarrow{IA}=-\frac{IA}{IM}.\overrightarrow{IM}=-\frac{IA}{IM}\left(\frac{BM}{a}.\overrightarrow{IC}+\frac{CM}{a}.\overrightarrow{IB}\right)\)
\(=-\frac{S_B+S_C}{S_A}\left(\frac{S_C}{S_B+S_C}.\overrightarrow{IC}+\frac{S_B}{S_B+S_C}.\overrightarrow{IB}\right)\)
\(=-\left(\frac{S_C}{S_A}.\overrightarrow{IC}+\frac{S_B}{S_A}.\overrightarrow{IB}\right)=-\left(\frac{c}{a}.\overrightarrow{IC}+\frac{b}{a}.\overrightarrow{IB}\right)\)
\(\Rightarrow a.\overrightarrow{IA}=-\left(b.\overrightarrow{IB}+c.\overrightarrow{IC}\right)\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\overrightarrow{0}\)(đpcm).