Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

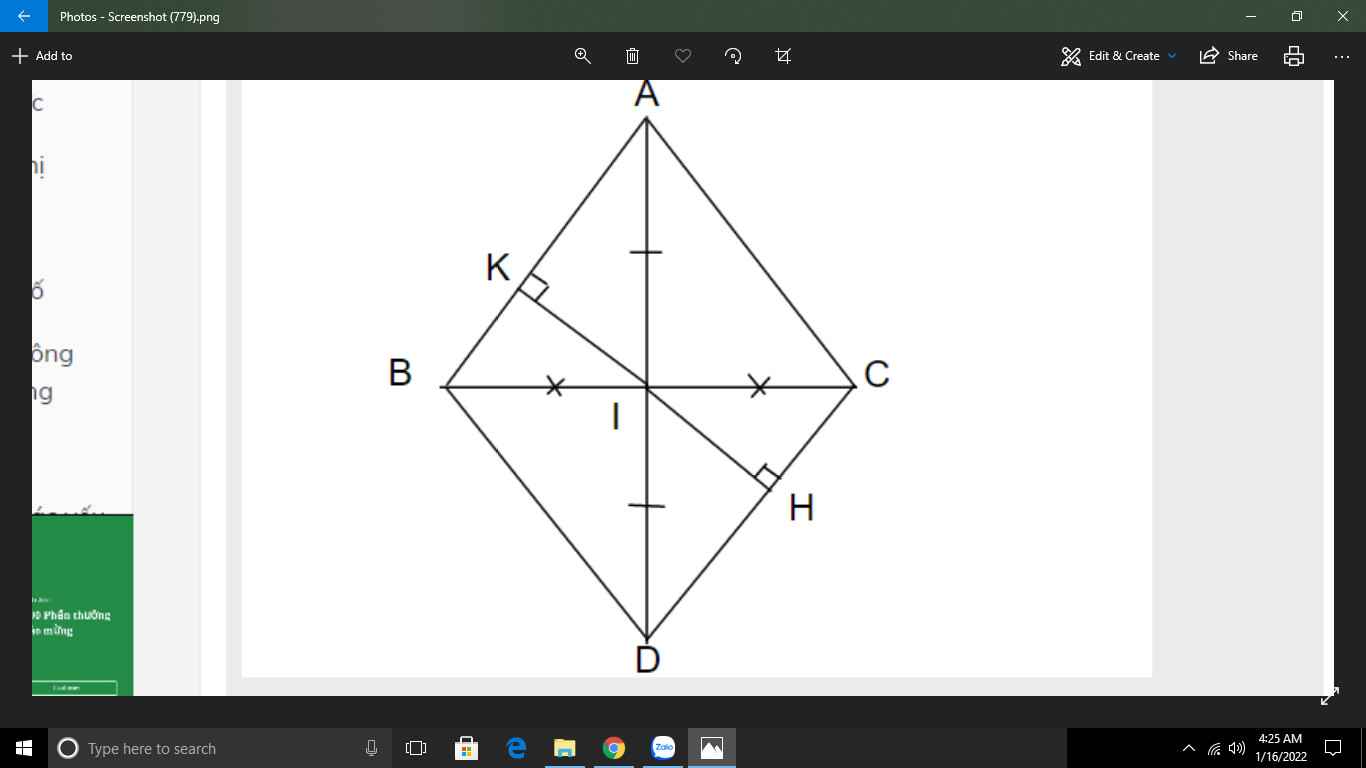
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

Để giải bài toán này, ta có thể sử dụng các định lý và tính chất trong hình học Euclid. Dưới đây là cách chứng minh cho từng phần:
a) Chứng minh tam giác AIB = tam giác AIC:
Ta có AB = AC (do đề bài cho)IA = IA (do cùng là một đoạn)IB = IC (do I là trung điểm của BC)Vậy tam giác AIB và tam giác AIC bằng nhau theo nguyên lý cạnh - cạnh - cạnh.b) Chứng minh AI là tia phân giác của góc BAC:
Do tam giác AIB = tam giác AIC nên ∠BAI = ∠CAIVậy AI là tia phân giác của góc BAC.c) Chứng minh IA là tia phân giác của góc HIK:
Do IH vuông góc AB và IK vuông góc AC nên ∠HIK = 90° + ∠BACMà AI là tia phân giác của góc BAC nên ∠HIA = ∠KIA = 1/2 ∠BACVậy ∠HIA + ∠KIA = ∠HIKVậy IA là tia phân giác của góc HIK.a: Xét ΔAIB và ΔAIC có
AB=AC
IB=IC
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của \(\widehat{BAC}\)
c: Xét ΔAIH vuông tại H và ΔAIK vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAIH=ΔAIK
=>\(\widehat{HIA}=\widehat{KIA}\)
=>IA là phân giác của \(\widehat{HIK}\)

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

A B C I H K D
a, Xét △ABI và △ACI có :
AB = AC (gt)
BI = CI (do I là trung điểm BC)
AI chung
=> △ABI = △ACI (c-c-c)
b, Xét △AIC và △DIB có :
AI = DI (gt)
\(\widehat{AIC}=\widehat{DIB}\) (đối đỉnh)
IC = IB
=> △AIC = △DIB (c-g-c)
=> \(\widehat{DBI}=\widehat{ICA}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AC // BD
c, Xét △IKB và △IHC có :
\(\widehat{IKB}=\widehat{IHC}=90^O\)
IB = IC
\(\widehat{KIB}=\widehat{CIH}\) (đối đỉnh)
=> △IKB = △IHC (ch-gn)
=> IK = IH

a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét ΔABI và ΔDCI có
AI=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔABI=ΔDCI
Suy ra: AB=CD
Xét △ABI và △ACI có :
AB = AC (gt)
BI = CI (do I là trung điểm BC)
AI chung
=> △ABI = △ACI (c-c-c)
Xét △AIC và △DIB có :
AI = DI (gt)
ˆAIC=ˆDIBAIC^=DIB^ (đối đỉnh)
IC = IB
=> △AIC = △DIB (c-g-c)
=> ˆDBI=ˆICADBI^=ICA^ (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AC // BD
Xét △IKB và △IHC có :
ˆIKB=ˆIHC=90OIKB^=IHC^=90O
IB = IC
ˆKIB=ˆCIHKIB^=CIH^ (đối đỉnh)
=> △IKB = △IHC (ch-gn)
=> IK = IH