Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

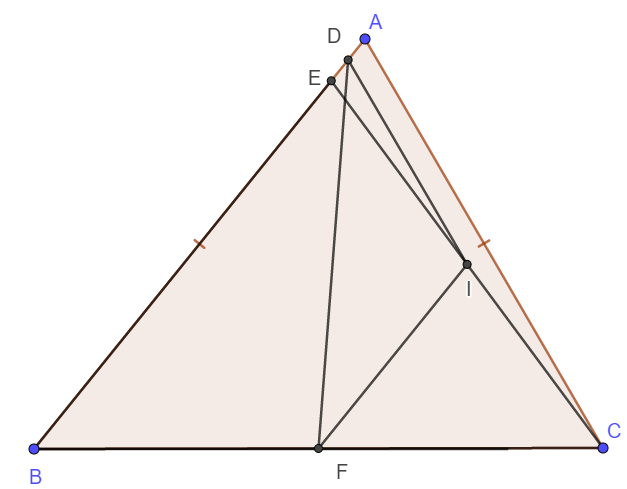
a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)

a) Xét tứ giác AMDN, ta có:
^A = ^N = ^M = 90o (gt)
Vậy tứ giác AMDN là hình chữ nhật.
b) *Xét △ABD, ta có:
K là trung điểm BD (gt)
I là trung điểm AD (gt)
⇒ KI là đường trung bình của △ABD.
⇒ KI // AB và KI = 12
AB. (1)
*Ta có:
DN ⊥ AC (gt)
AB ⊥ AC (△ABC vuông tại A)
⇒ DN // AB. (2)
Từ (1) và (2) suy ra KI // DN
*Xét △v ABC, ta có:
BD = CD (gt)
⇒ AD là đường trung tuyến
⇒ AD = BD = 12
AC
⇒ △ABD cân tại D
Mà DM ⊥ AB
⇒ DM là đường cao đồng thời là đường trung tuyến
⇒ MA = MB
*Ta có:
MA = 12
AB (cmt)
KI = 12
AB (cmt)
⇒MA = KI
Mà MA = DN (AMDN là hình chữ nhật)
Nên KI = DN
*Ta có:
KI // DN (cmt)
KI = DN (cmt)
Vậy INDK là hình bình hành
c) *Ta có:
KI //AM (KI // AB)
DM ⊥ AM (gt)
⇒KI ⊥ DM
*Xét tứ giác DIMK, ta có:
KI ⊥ DM (cmt)
Vậy DIMK là hình thoi.
d) Xét hình chữ nhật AMDN, ta có:
MN, AD là hai đường chéo
Mà I là trung điểm AD (gt)
Nên I là trung điểm MN
Vậy M, N đối xứng với nhau qua I.